Geophysical Inversion and Modelling Library v1.5.4
Loading...
Searching...
No Matches
Public Member Functions | Protected Member Functions | Protected Attributes | List of all members
GIMLI::PolynomialFunction< ValueType > Class Template Reference

#include <polynomial.h>

Public Member Functions

 PolynomialFunction (uint size=0)
 
 PolynomialFunction (const Vector< ValueType > &ax)
 
 PolynomialFunction (const Vector< ValueType > &ax, const Vector< ValueType > &ay)
 
 PolynomialFunction (const Vector< ValueType > &ax, const Vector< ValueType > &ay, const Vector< ValueType > &az)
 
RMatrix & operator[] (Index k)
 
const RMatrix & operator[] (Index k) const
 
RMatrix & matR (Index k)
 
ValueType operator() (const Pos &xyz) const
 
Vector< ValueType > operator() (const std::vector< Pos > &xyz) const
 
Index size () const
 
PolynomialFunction< ValueType > derive (uint dim) const
 
void fillElementList ()
 
const std::vector< PolynomialElement< ValueType > > & elements () const
 
void clear ()
 
PolynomialFunction< ValueType > & fill (const Vector< ValueType > &c)
 
RVector coeff () const
 

Protected Member Functions

void init_ (const Vector< ValueType > &ax, const Vector< ValueType > &ay, const Vector< ValueType > &az)
 

Protected Attributes

std::vector< Matrix< ValueType > > mat_
 
std::vector< PolynomialElement< ValueType > > elementList_
 

Detailed Description

template<class ValueType>
class GIMLI::PolynomialFunction< ValueType >

Three dimensional polynomial function. For symbolic calculation and derivation. I.e. f(x,y,z) = 1 + x + y + z + xy + xz + zz ...

Constructor & Destructor Documentation

◆ PolynomialFunction() [1/4]

template<class ValueType>
GIMLI::PolynomialFunction< ValueType >::PolynomialFunction ( uint size = 0)
inline

Create empty polynomial

◆ PolynomialFunction() [2/4]

template<class ValueType>
GIMLI::PolynomialFunction< ValueType >::PolynomialFunction ( const Vector< ValueType > & ax)
inline

Create a polynomial 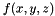$ f(x,y,z) $ from one dimensional polynomial coefficient array ax: $ f(x,y,z) = ax[0] + ax[1]x + ax[2]x^2 ... $

◆ PolynomialFunction() [3/4]

template<class ValueType>
GIMLI::PolynomialFunction< ValueType >::PolynomialFunction ( const Vector< ValueType > & ax,
const Vector< ValueType > & ay )
inline

Create a polynomial function 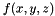$ f(x,y,z) $ from one dimensional polynomial coefficient array ax and ay: $ f(x,y,z) = ax[0] + ax[1]x + ax[2]x^2 + ... + ay[0] + ay[1]y + ay[2]y^2 + ... $. If u need a composed polynomial use f(x,y,z)*g(x,y,z).

◆ PolynomialFunction() [4/4]

template<class ValueType>
GIMLI::PolynomialFunction< ValueType >::PolynomialFunction ( const Vector< ValueType > & ax,
const Vector< ValueType > & ay,
const Vector< ValueType > & az )
inline

Create a polynomial function 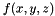$ f(x,y,z) $ from one dimensional polynomial coefficient array ax, ay, az: $ f(x,y,z) = ax[0] + ax[1]x + ax[2]x^2 + ... + ay[0] + ay[1]y + ay[2]y^2 + ... + az[0] + az[1]z + az[2]z^2 + ... $ If u need a composed polynomial use f(x,y,z)*g(x,y,z)*h(x,y,z).

Member Function Documentation

◆ coeff()

template<class ValueType>
RVector GIMLI::PolynomialFunction< ValueType >::coeff ( ) const
inline

Return all coefficients.

◆ derive()

template<class ValueType>
PolynomialFunction< ValueType > GIMLI::PolynomialFunction< ValueType >::derive ( uint dim) const
inline

Create new polynomial function for 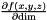$ \frac{\partial f(x,y,z)}{\partial \mathrm{dim}}$

Parameters
dim= 0 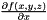$ \frac{\partial f(x,y,z)}{\partial x}$
dim= 1 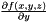$ \frac{\partial f(x,y,z)}{\partial y}$
dim= 2 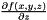$ \frac{\partial f(x,y,z)}{\partial z}$

◆ fill()

template<class ValueType>
PolynomialFunction< ValueType > & GIMLI::PolynomialFunction< ValueType >::fill ( const Vector< ValueType > & c)
inline

Fill the parameter coefficients from array. If c.size() == this.size()^3. mat_[k][i][j] = c[k*(size() * size())+ j * size() + i] and return the PolynomialFunction itself. If c.size() is size of elementList_, assume that only the values from elementList_ will be exchanged. Please note, all values of c will be snapped to tolerance.

◆ matR()

template<class ValueType>
RMatrix & GIMLI::PolynomialFunction< ValueType >::matR ( Index k)
inline

Return reference to f(x, y, z[k]) polynomial matrix. For python only

◆ operator()() [1/2]

template<class ValueType>
ValueType GIMLI::PolynomialFunction< ValueType >::operator() ( const Pos & xyz) const
inline

Evaluate f(x,y,z)

◆ operator()() [2/2]

template<class ValueType>
Vector< ValueType > GIMLI::PolynomialFunction< ValueType >::operator() ( const std::vector< Pos > & xyz) const
inline

Evaluate f(x_i,y_i,z_i) for i = [0 .. xyz.size()).

◆ operator[]() [1/2]

template<class ValueType>
RMatrix & GIMLI::PolynomialFunction< ValueType >::operator[] ( Index k)
inline

Return f(x, y, z[k]) polynomial matrix

◆ operator[]() [2/2]

template<class ValueType>
const RMatrix & GIMLI::PolynomialFunction< ValueType >::operator[] ( Index k) const
inline

Return f(x, y, z[k]) polynomial matrix

◆ size()

template<class ValueType>
Index GIMLI::PolynomialFunction< ValueType >::size ( ) const
inline

Return the size of this polynomial.

Referenced by GIMLI::operator*().