A Shape defines a geometrical primitive. More...

#include <shape.h>

Inherited by GIMLI::EdgeShape, GIMLI::HexahedronShape, GIMLI::NodeShape, GIMLI::PolygonShape, GIMLI::PyramidShape, GIMLI::QuadrangleShape, GIMLI::TetrahedronShape, GIMLI::TriPrismShape, and GIMLI::TriangleShape.

Collaboration diagram for GIMLI::Shape:

Public Member Functions
	Shape (MeshEntity *ent)

virtual	~Shape ()

virtual int	rtti () const =0

virtual int	dim () const =0

virtual std::string	name () const

Index	nodeCount () const

Node &	node (Index i) const

void	setNodesPtr (const std::vector< Node * > &n)

const std::vector< Node * > &	nodes () const

virtual std::vector< PolynomialFunction< double > >	createShapeFunctions () const

void	createJacobian (RMatrix3 &J) const

RMatrix3	createJacobian () const

const RMatrix3 &	invJacobian () const

virtual RVector	N (const RVector3 &L) const

virtual void	N (const RVector3 &L, RVector &ret) const

virtual void	dNdrst (const RVector3 &rst, RMatrix &MdNdrst) const

virtual RMatrix	dNdrst (const RVector3 &L) const

virtual void	rst2xyz (const RVector3 &rst, RVector3 &xyz) const

virtual RVector3	xyz (const RVector3 &rst) const

virtual void	xyz2rst (const RVector3 &xyz, RVector3 &rst) const

virtual RVector3	rst (const RVector3 &xyz) const

virtual RVector3	rst (Index i) const

double	drstdxyz (uint rstI, uint xyzJ) const

virtual bool	isInside (const RVector3 &xyz, bool verbose=false) const

virtual bool	isInside (const RVector3 &xyz, RVector &sf, bool verbose=false) const

virtual bool	touch (const RVector3 &pos, double tol=1e-6, bool verbose=false) const

virtual bool	intersectRay (const RVector3 &start, const RVector3 &dir, RVector3 &pos)

double	domainSize () const

RVector3	center () const

virtual RVector3	norm () const

double	h () const

virtual Plane	plane () const

void	changed ()

double	jacobianDeterminant () const

void	resizeNodeSize_ (Index n)

Protected Member Functions
virtual double	domainSize_ () const

Protected Attributes
Index	nodeCount_

double	domSize_

bool	hasDomSize_

double	_h

RMatrix3	invJacobian_

const std::vector< Node * > *	nodeVector_

Detailed Description

A Shape defines a geometrical primitive.

A Shape defines a geometrical primitive. And is the geometrical base of a MeshEntity.

Constructor & Destructor Documentation

◆ Shape()

GIMLI::Shape::Shape ( MeshEntity * ent )

Default constructor.

References setNodesPtr().

◆ ~Shape()

GIMLI::Shape::~Shape ( )

virtual

Default destructor.

Member Function Documentation

◆ center()

RVector3 GIMLI::Shape::center ( ) const

Returns the middle position of this shape

References center(), node(), and nodeCount().

Referenced by center().

◆ changed()

void GIMLI::Shape::changed ( )

Notify this shape that the inverse Jacobian matrix and the domain size are not longer valid and need recalculation. This method is called if a node has bee transformed.

◆ createJacobian()

void GIMLI::Shape::createJacobian ( RMatrix3 & J ) const

Create and return the Jacobian matrix for this shape at the local coordinate $ L[r,s,t]$ .
The Jacobian matrix is a 3x3 matrix representing the absolute derivative matrix for this shape regarding the $\mathcal{N}$ shape functions:

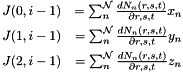
$\begin{eqnarray*} J(0,i-1) & = \sum_n^{\mathcal{N}}\frac{dN_n(r,s,t)}{\partial r,s,t}x_n \\ J(1,i-1) & = \sum_n^{\mathcal{N}}\frac{dN_n(r,s,t)}{\partial r,s,t}y_n \\ J(2,i-1) & = \sum_n^{\mathcal{N}}\frac{dN_n(r,s,t)}{\partial r,s,t}z_n \end{eqnarray*}$

for i = [1,2,3]

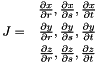
$\begin{eqnarray*} & \frac{\partial x}{\partial r}, \frac{\partial x}{\partial s}, \frac{\partial x}{\partial t}\\ J = & \frac{\partial y}{\partial r}, \frac{\partial y}{\partial s}, \frac{\partial y}{\partial t}\\ & \frac{\partial z}{\partial r}, \frac{\partial z}{\partial s}, \frac{\partial z}{\partial t}\\ \end{eqnarray*}$

the inverse of the Jacobian results in:

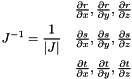
$\begin{eqnarray*} & \frac{\partial r}{\partial x}, \frac{\partial r}{\partial y}, \frac{\partial r}{\partial z}\\ J^{-1} = \frac{1}{|J|} & \frac{\partial s}{\partial x}, \frac{\partial s}{\partial y}, \frac{\partial s}{\partial z}\\ & \frac{\partial t}{\partial x}, \frac{\partial t}{\partial y}, \frac{\partial t}{\partial z} \end{eqnarray*}$

References createJacobian(), dNdrst(), GIMLI::Singleton< ShapeFunctionCache >::instance(), node(), nodeCount(), rtti(), GIMLI::x(), GIMLI::y(), and GIMLI::z().

Referenced by createJacobian(), and invJacobian().

◆ createShapeFunctions()

std::vector< PolynomialFunction< double > > GIMLI::Shape::createShapeFunctions ( ) const

virtual

Return a reference to all nodes.

Reimplemented in GIMLI::TriPrismShape.

References rtti().

◆ dNdrst()

void GIMLI::Shape::dNdrst	(	const RVector3 &	rst,
		RMatrix &	MdNdrst ) const

virtual

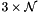
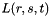
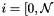
Return the derivative matrix of size ( $3\times\mathcal{N}$ ) for the shape functions at the local coordinate. $ L(r,s,t) $ . Result is independent of L for linear shape function (TODO Remove on cleanup) $[[\frac{dN_i(r,s,t)}{\partial r}],[\frac{dN_i(r,s,t)}{\partial s}],[\frac{dN_i(r,s,t)}{\partial t}]^{\mathrm{T}}]$ for $i = [0,\mathcal{N}$

References GIMLI::Singleton< ShapeFunctionCache >::instance(), and rst().

Referenced by createJacobian().

◆ domainSize()

double GIMLI::Shape::domainSize ( ) const

Get the domain size of this shape, i.e., length, area or volume

References domainSize_().

◆ domainSize_()

virtual double GIMLI::Shape::domainSize_ ( ) const

inlineprotectedvirtual

Virtual method to calculate the domain size i.e length, area, volume of the shapes

Reimplemented in GIMLI::EdgeShape, GIMLI::HexahedronShape, GIMLI::NodeShape, GIMLI::QuadrangleShape, GIMLI::TetrahedronShape, GIMLI::TriangleShape, and GIMLI::TriPrismShape.

Referenced by domainSize().

◆ drstdxyz()

double GIMLI::Shape::drstdxyz	(	uint	rstI,
		uint	xyzJ ) const

inline

Return derivative from local coordinates to Cartesian coordinates. These are the elements of the inverse Jacobian matrix.

References invJacobian().

◆ h()

double GIMLI::Shape::h ( ) const

Returns maximum distance between 2 nodes.

References node(), and nodeCount().

◆ intersectRay()

virtual bool GIMLI::Shape::intersectRay	(	const RVector3 &	start,
		const RVector3 &	dir,
		RVector3 &	pos )

inlinevirtual

Return true if the ray intersects the shape. On boundary means inside too. The intersection position is stored in pos.

Reimplemented in GIMLI::EdgeShape, GIMLI::QuadrangleShape, and GIMLI::TriangleShape.

References name(), and rtti().

Referenced by GIMLI::Mesh::findCellsAlongRay().

◆ invJacobian()

const RMatrix3 & GIMLI::Shape::invJacobian ( ) const

Return the inverse of the Jacobian Matrix. And create and cache it on demand. The matrix is no more valid if the shape was transformed.

References createJacobian(), GIMLI::Singleton< ShapeFunctionCache >::instance(), and GIMLI::inv().

Referenced by drstdxyz(), and xyz2rst().

◆ isInside() [1/2]

bool GIMLI::Shape::isInside	(	const RVector3 &	xyz,
		bool	verbose = false ) const

virtual

Return true if the Cartesian coordinates xyz are inside the shape. On boundary means inside too. Works only for shapes dedicated as cells because they need to be aligned to the dimension. See also touch.

Reimplemented in GIMLI::PolygonShape.

References isInside(), and xyz().

Referenced by GIMLI::QuadrangleShape::intersectRay(), GIMLI::TriangleShape::intersectRay(), and isInside().

◆ isInside() [2/2]

bool GIMLI::Shape::isInside	(	const RVector3 &	xyz,
		RVector &	sf,
		bool	verbose = false ) const

virtual

Return true if the Cartesian coordinates xyz are inside the shape. On boundary means inside too. sf contains the complete shape function to identify next neighbor. Works only for shapes dedicated as cells because they need to be aligned to the dimension. See also touch.

References N(), rst(), and xyz().

◆ N() [1/2]

RVector GIMLI::Shape::N ( const RVector3 & L ) const

virtual

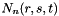
Return a RVector for the $n=[0,\mathrm{nodeCount()}]$ shape functions $ N_n(r,s,t)$ at the local coordinate $ L(r,s,t)$ .

References N(), nodeCount(), and rst().

Referenced by isInside(), N(), N(), and rst2xyz().

◆ N() [2/2]

void GIMLI::Shape::N	(	const RVector3 &	L,
		RVector &	ret ) const

virtual

TODO replace this with expressions.
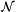
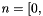
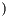
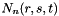
Fill the allocated RVector n of size $\mathcal{N}$ for the $ n=[0,$ \mathcal{N} $) $ shape functions $ N_n(r,s,t)$ for the local coordinate $ L(r,s,t)$ . For performance reasons the size of L will not be checked. This method needs to be specialized in the corresponding child classes.

References GIMLI::Singleton< ShapeFunctionCache >::instance(), N(), and rst().

◆ name()

virtual std::string GIMLI::Shape::name ( ) const

inlinevirtual

Return an identification name for the shape.

Reimplemented in GIMLI::EdgeShape, GIMLI::HexahedronShape, GIMLI::NodeShape, GIMLI::PolygonShape, GIMLI::QuadrangleShape, GIMLI::TetrahedronShape, GIMLI::TriangleShape, and GIMLI::TriPrismShape.

Referenced by intersectRay().

◆ node()

Node & GIMLI::Shape::node ( Index i ) const

Return a read only reference to the i-th Node of this shape.

References nodeCount().

Referenced by center(), createJacobian(), h(), GIMLI::EdgeShape::intersectRay(), GIMLI::QuadrangleShape::intersectRay(), GIMLI::TriangleShape::intersectRay(), GIMLI::EdgeShape::norm(), GIMLI::QuadrangleShape::norm(), GIMLI::TriangleShape::norm(), plane(), rst2xyz(), GIMLI::EdgeShape::touch(), touch(), GIMLI::TetrahedronShape::volume(), GIMLI::TetrahedronShape::xyz2rst(), and GIMLI::TriangleShape::xyz2rst().

◆ nodeCount()

Index GIMLI::Shape::nodeCount ( ) const

inline

Return the amount of nodes for this shape.

Referenced by center(), createJacobian(), GIMLI::Mesh::createNeighborInfosCell_(), h(), N(), node(), plane(), GIMLI::EdgeShape::rst(), GIMLI::HexahedronShape::rst(), GIMLI::PyramidShape::rst(), GIMLI::QuadrangleShape::rst(), GIMLI::TetrahedronShape::rst(), GIMLI::TriangleShape::rst(), GIMLI::TriPrismShape::rst(), rst2xyz(), and touch().

◆ nodes()

const std::vector< Node * > & GIMLI::Shape::nodes ( ) const

inline

Return a read only reference to all nodes.

◆ norm()

RVector3 GIMLI::Shape::norm ( ) const

virtual

Returns the norm vector if possible otherwise returns non valid Vector3

Reimplemented in GIMLI::EdgeShape, GIMLI::NodeShape, GIMLI::PolygonShape, GIMLI::QuadrangleShape, and GIMLI::TriangleShape.

Referenced by plane().

◆ plane()

Plane GIMLI::Shape::plane ( ) const

virtual

Returns the a plane for this shape if its possible (2D or 3D plane shapes) otherwise returns non valid Plane.

References GIMLI::Pos::abs(), node(), nodeCount(), norm(), and plane().

Referenced by GIMLI::Mesh::copyBoundary(), GIMLI::QuadrangleShape::intersectRay(), GIMLI::TriangleShape::intersectRay(), GIMLI::PolygonShape::norm(), plane(), and touch().

◆ rst() [1/2]

RVector3 GIMLI::Shape::rst ( const RVector3 & xyz ) const

virtual

Return local coordinates for Cartesian coordinates regarding the shape function.

References rst(), xyz(), and xyz2rst().

Referenced by dNdrst(), GIMLI::Mesh::interpolationMatrix(), isInside(), N(), N(), rst(), rst2xyz(), xyz(), and xyz2rst().

◆ rst() [2/2]

RVector3 GIMLI::Shape::rst ( Index i ) const

virtual

Return local coordinates for node i.

Reimplemented in GIMLI::EdgeShape, GIMLI::HexahedronShape, GIMLI::NodeShape, GIMLI::PolygonShape, GIMLI::PyramidShape, GIMLI::QuadrangleShape, GIMLI::TetrahedronShape, GIMLI::TriangleShape, and GIMLI::TriPrismShape.

References rtti().

◆ rst2xyz()

void GIMLI::Shape::rst2xyz	(	const RVector3 &	rst,
		RVector3 &	xyz ) const

virtual

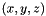
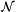
Perform coordinate transformation from the locale coordinates $ (r,s,t)=(r,s,t)=([0..1,0..1,0..1]) $ of this shape to Cartesian coordinates $ (x,y,z) $ regarding to the $\mathcal{N}$ shape functions N $ N_i $ with $i=[0,\mathcal{N})$
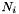
This is the opposite to xyz2rst().

$\begin{eqnarray*} x &=& \sum_i^{\mathcal{N}} N_i(r,s,t)x_i \\ y &=& \sum_i^{\mathcal{N}} N_i(r,s,t)y_i \\ z &=& \sum_i^{\mathcal{N}} N_i(r,s,t)z_i \end{eqnarray*}$

This is a generic function and may be overwritten by faster methods for shape simplexes.

References N(), node(), nodeCount(), rst(), and xyz().

Referenced by xyz().

◆ rtti()

virtual int GIMLI::Shape::rtti ( ) const

pure virtual

Pure virtual methode for runtime identification.

Implemented in GIMLI::EdgeShape, GIMLI::HexahedronShape, GIMLI::NodeShape, GIMLI::PolygonShape, GIMLI::PyramidShape, GIMLI::QuadrangleShape, GIMLI::TetrahedronShape, GIMLI::TriangleShape, and GIMLI::TriPrismShape.

Referenced by GIMLI::IntegrationRules::abscissa(), createJacobian(), createShapeFunctions(), intersectRay(), rst(), and GIMLI::IntegrationRules::weights().

◆ setNodesPtr()

void GIMLI::Shape::setNodesPtr ( const std::vector< Node * > & n )

inline

Return a reference to the i-th Node of this shape.

Set the ptr to nodes array from, which the MeshEntity holds.

Referenced by Shape().

◆ touch()

bool GIMLI::Shape::touch	(	const RVector3 &	pos,
		double	tol = 1e-6,
		bool	verbose = false ) const

virtual

Check if the position touches the entity. Works only for shapes dedicated as boundaries. On edge of the boundary means inside too. See also isInside.

Reimplemented in GIMLI::EdgeShape.

References GIMLI::Pos::dist(), GIMLI::Line::intersectRay(), node(), nodeCount(), plane(), GIMLI::Line::t(), GIMLI::Plane::touch(), and touch().

Referenced by GIMLI::Mesh::copyBoundary(), and touch().

◆ xyz()

RVector3 GIMLI::Shape::xyz ( const RVector3 & rst ) const

virtual

Return the Cartesian coordinates for the locale coordinates rst. See rst2xyz.

References rst(), rst2xyz(), and xyz().

Referenced by GIMLI::calcGCells(), GIMLI::Mesh::createRefined_(), GIMLI::evaluateQuadraturePoints(), GIMLI::evaluateQuadraturePoints(), GIMLI::evaluateQuadraturePoints(), GIMLI::PolygonShape::isInside(), isInside(), isInside(), rst(), rst2xyz(), xyz(), and xyz2rst().

◆ xyz2rst()

void GIMLI::Shape::xyz2rst	(	const RVector3 &	xyz,
		RVector3 &	rst ) const

virtual

Convert Cartesian coordinates into locale coordinates regarding the shape functions. This is the opposite to xyz2rst. This is a generic function and may be overwritten by faster methods for shape simplexes. Solve the nonlinear system of equations by newton method 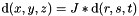$\mathrm{d}(x,y,z)= J*\mathrm{d}(r,s,t)$

Reimplemented in GIMLI::TetrahedronShape, and GIMLI::TriangleShape.

References GIMLI::Pos::abs(), invJacobian(), rst(), and xyz().

Referenced by rst().

Public Member Functions

Protected Member Functions

Protected Attributes

Detailed Description

Constructor & Destructor Documentation

◆ Shape()

◆ ~Shape()

Member Function Documentation

◆ center()

◆ changed()

◆ createJacobian()

◆ createShapeFunctions()

◆ dNdrst()

◆ domainSize()

◆ domainSize_()

◆ drstdxyz()

◆ h()

◆ intersectRay()

◆ invJacobian()

◆ isInside() [1/2]

◆ isInside() [2/2]

◆ N() [1/2]

◆ N() [2/2]

◆ name()

◆ node()

◆ nodeCount()

◆ nodes()

◆ norm()

◆ plane()

◆ rst() [1/2]

◆ rst() [2/2]

◆ rst2xyz()

◆ rtti()

◆ setNodesPtr()

◆ touch()

◆ xyz()

◆ xyz2rst()