Matrices

There is a large number of Matrix types that are all derived from the base class MatrixBase. They do not have to store elements but can be logical or wrappers. They just have to provide the functions A.cols(), A.rows() (column and row numbers), A.mult(x)\(=A\cdot x\) and A.transMult(y)\(=A^T\cdot y\).

# We start off with the typical imports
import numpy as np
import pygimli as pg

Dense matrix Matrix

All elements are stored column-wise, i.e. all rows A[i] are of type pg.Vector. This matrix is used for storing dense data (like ERT Jacobians) and doing simple algebra.

A = pg.Matrix(3, 4)
A[0, 0] = 1
A[2, 2] = -1
A[1] = np.arange(4)
print(A)
x = np.arange(4) + 5
A*x

RMatrix: 3 x 4
4 [1.0, 0.0, 0.0, 0.0]
4 [0.0, 1.0, 2.0, 3.0]
4 [0.0, 0.0, -1.0, 0.0]


3 [5.0, 44.0, -7.0]

Exists also as complex matrix under pg.matrix.CMatrix.

Index-based sparse matrix SparseMapMatrix

Sparse matrix (most elements are zero) with single access and. Typical for traveltime Jacobian (only certain cells covered by individual rays) or constraint matrices.

A = pg.SparseMapMatrix(2, 3)
A.setVal(0, 0, -1)
A.setVal(0, 1, +1)  # first-order derivative
A.setVal(1, 0, -1)
A.setVal(1, 1, +2)
A.setVal(1, 2, -1)  # second-order derivative
x = [10, 12, 13]
print(A * x)
ax, _ = pg.show(A)

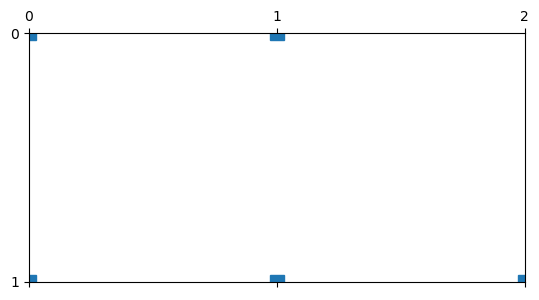
2 [2.0, 1.0]

Exists also as complex-valued variant pg.matrix.CSparseMapMatrix.

Column-compressed matrix SparseMatrix

Used for numerical approximation of partial differential equations like finite-element or finite volume. Not typically used unless efficiency is of importance. It exists also complex-valued as pg.matrix.CSparseMatrix.

Diagonal matrices

First, there is an identity matrix IdentityMatrix. No elements stored at all. Important for constraint matrices when combined into BlockMatrix (see below). More generally, there is a diagonal matrix DiagonalMatrix where only its diagonal is stored as vector.

A = pg.matrix.IdentityMatrix(3)  # , 2.0)
x = [10, 11, 12]
A*x

3 [10.0, 11.0, 12.0]

Weighted matrices

MultLeftMatrix/MultRightMatrix/MultLeftRightMatrix

Often, matrices are weighted from either side by a vector, e.g. data error weighting of the Jacobian matrix, data and model transformations, or weighting individual smoothness parts according to the roughness so that only the weighting is changed and not the matrix.

A = pg.Matrix(3, 4)
A += 1
w = [2, 3, -1]
B = pg.matrix.MultLeftMatrix(A, w)
x = np.arange(4)
print(A*x)
print(B*x)

3 [6.0, 6.0, 6.0]
3 [12.0, 18.0, -6.0]

Combinations of matrices

Logical matrices can combine different other matrices (of arbitrary type) avoiding double memory storage by multiplication (Mult2Matrix) or addition (Add2Matrix).

A = pg.Matrix(2, 3)
A += 1
B = pg.SparseMapMatrix(3, 4)
C = pg.matrix.Mult2Matrix(A, B)
x = np.arange(4)
C * x

2 [0.0, 0.0]

Block matrices

The most important type is the BlockMatrix, where arbitrary matrices are combined into a logical matrix. This is of importance for inversion frameworks: * joint inversion: Jacobian matrices are concatenated * combination of different constrains: combining different regularization * laterally, spatially or temporally constrained inversion: regularization between model cells of each frame but also between the frames Note that the matrices only have to be defined once and can appear multiply.

A = pg.BlockMatrix()
A1 = pg.Matrix(2, 2)
A.addMatrix(A1, 0, 0)
A.addMatrix(A1, 4, 0, scale=2.0)
A2 = pg.matrix.IdentityMatrix(5)
A.addMatrix(A2, 1, 2)
A3 = pg.SparseMapMatrix(2, 3)
A.addMatrix(A3, 2, 3)
print(A)
ax, _ = pg.show(A)

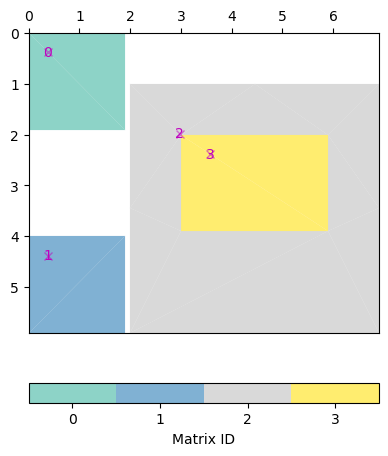
pg.matrix.BlockMatrix of size 6 x 7 consisting of 4 submatrices.

Matrix combinations

There are also simpler types of matrix combinations: * H2Matrix/V2Matrix: two matrices below/next to each other * HNMatrix/VNMatrix: one matrix repeated N times horizontally/vertically * NDMatrix: block diagonal matrix

Matrix wrappers

TransposedMatrix avoids transposing any matrix by exchanging left/right mult. SquaredMatrix keeps only the matrix A but works as A^T @ A SquaredTransposeMatrix keeps only the matrix A but works as A @ A.T RealNumpyMatrix holds a real-valued numpy array ComplexNumpyMatrix holds a complex-valued numpy array in a real pg matrix NumpyMatrix

Matrix generators

Often, several matrices or even the same one have to be combined. RepeatHMatrix, RepeatVMatrix, RepeatDMatrix hold a single matrix that is repeated horizontally, vertically or diagonally. NDMatrix, FrameConstraintMatrix is a special generator for constraining cells of every (e.g. timelapse) frame and moreover the frames with each other.

F = pg.matrix.FrameConstraintMatrix(A3, 3)
ax, _ = pg.show(F)
print(F)

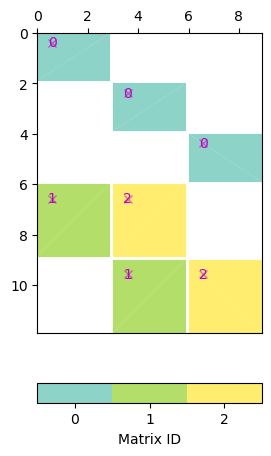
pg.matrix.BlockMatrix of size 12 x 9 consisting of 7 submatrices.

Geostatistical constraint matrix

For geostatistical constraints, a correlation matrix is computed using correlation lengths and angles to define their directions. To access its inverse root in a way that avoids matrix inversion, an eigenvalue decomposition is done and the eigenvalues \(D`\) and -vectors \(Q\) are stored so that the operator

\[C^{-0.5}\cdot x=Q\cdot D^{-0.5}\cdot Q^T \cdot x\]

Jordi, C., Doetsch, J., Günther, T., Schmelzbach, C. & Robertsson, J.O.A. (2018): Geostatistical regularisation operators for geophysical inverse problems on irregular meshes. Geophysical Journal International 213, 1374- 1386, doi:10.1093/gji/ggy055.