Note
Go to the end to download the full example code.
Region-wise regularization#
In this tutorial we like to demonstrate how to control the regularization of subsurface regions individually by using an ERT field case. The data is a 2d profile that was measured in 2005 on the bottom of a lake. The water body is of course influencing the fields and needs to be treated accordingly.
We first import pygimli and the modules for ERT and mesh building.
import matplotlib.pyplot as plt
import pygimli as pg
from pygimli.physics import ert
import pygimli.meshtools as mt
Data and geometry#
The data was measured across a shallow lake with the most electrodes being on the bottom of a lake. We used cables with 2m spaced takeouts.
data = pg.getExampleData("ert/lake.ohm")
print(data)
Data: Sensors: 48 data: 658, nonzero entries: ['a', 'b', 'err', 'i', 'm', 'n', 'r', 'u', 'valid']
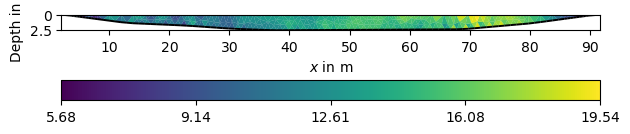
The data consists of 658 data with current and voltage using 48 electrodes. We first have a look at the electrode positions measured by a stick.
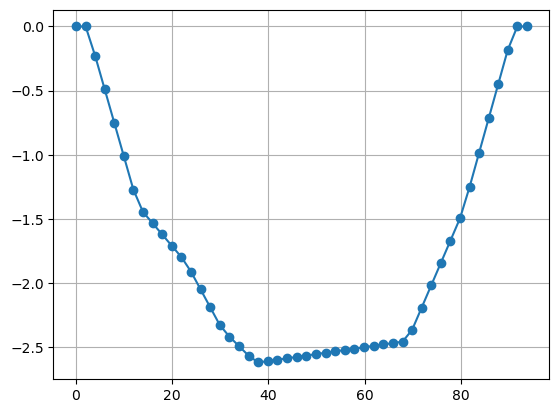
On both sides, two electrodes are on shore, but the others are on the bottom of a shallow lake with a maximum depth of 2.5m.
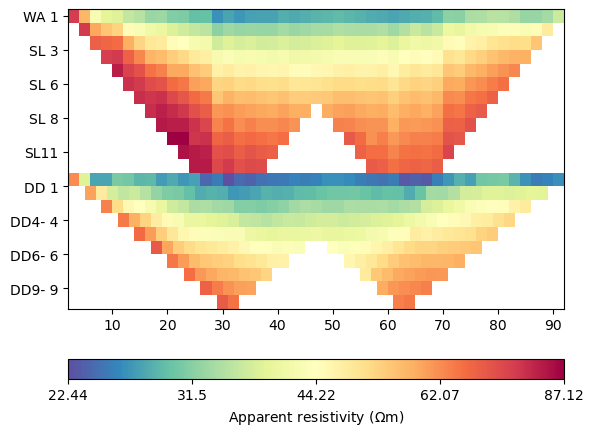
We combined Wenner-Schlumberger (top) and Wenner-beta (bottom) data. The lowest resistivities correspond with the water resistivity of 22.5 :math:`Omega`m.
The contained errors are measured standard devitations and should not be used for inversion. Instead, we estimate new errors using 2% and 100microVolts.
data["err"] = ert.estimateError(data, relativeError=0.02, absoluteUError=1e-4)
print(max(data["err"]))
# pg.show(data, data["err"]*100, label="error (%)");
0.02584795321637427
Building a mesh with the water body#
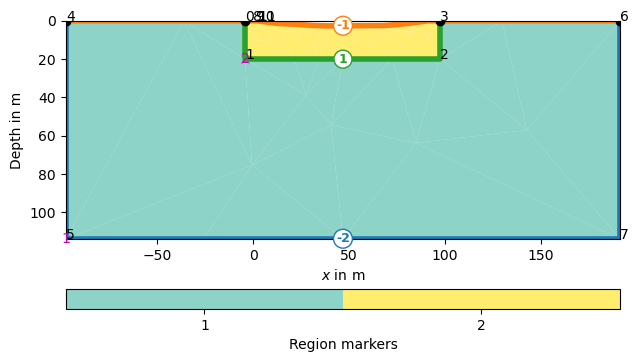
0 -4.0 0.0
1 -4.0 -20.0
2 97.7452 -20.0
3 97.7452 0.0
4 -97.7452 0.0
5 -97.7452 -113.7452
6 191.4904 0.0
7 191.4904 -113.7452
8 0.0 0.0
9 1.0 0.0
10 2.0 0.0
11 2.993365 -0.11499999999999999
So node number 10 is the left one at the shore
95 86.7804 -0.5833335
96 87.7715 -0.45
97 88.76255 -0.3166665
98 89.75359999999999 -0.183333
99 90.7494 -0.0916665
100 91.7452 0.0
101 92.7452 0.0
102 93.7452 0.0
and 100 the first on the other side. We connect nodes 10 and 100 by an edge
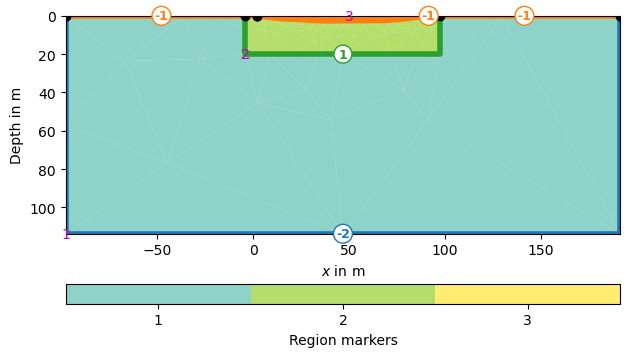
As the lake bottom is not a surface boundary (-1) anymore, but an inside boundary, we set its marker >0 by iterating through all boundaries.
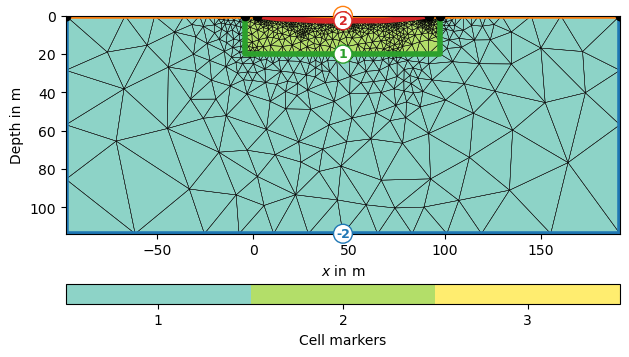
Mesh: Nodes: 1188 Cells: 2217 Boundaries: 3404
Inversion with the ERT manager#
mgr = ert.ERTManager(data, verbose=True)
mgr.setMesh(mesh) # use this mesh for all subsequent runs
mgr.invert()
# mgr.invert(mesh=mesh) would only temporally use the mesh
fop: <pygimli.physics.ert.ertModelling.ERTModelling object at 0x1731e7d30>
Data transformation: Logarithmic LU transform, lower bound 0.0, upper bound 0.0
Model transformation: Logarithmic transform
min/max (data): 22.44/87.12
min/max (error): 2%/2.58%
min/max (start model): 47.2/47.2
--------------------------------------------------------------------------------
inv.iter 0 ... chi² = 211.20
--------------------------------------------------------------------------------
inv.iter 1 ... chi² = 60.46 (dPhi = 71.32%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 2 ... chi² = 19.19 (dPhi = 67.98%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 3 ... chi² = 7.60 (dPhi = 59.40%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 4 ... chi² = 4.68 (dPhi = 37.47%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 5 ... chi² = 3.15 (dPhi = 31.23%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 6 ... chi² = 1.80 (dPhi = 39.57%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 7 ... chi² = 1.80 (dPhi = -0.28%) lam: 20.0
################################################################################
# Abort criterion reached: dPhi = -0.28 (< 2.0%) #
################################################################################
1751 [243.34025874242005,...,129.57343581818645]
The fit is obviously not perfect. So we have a look at data and model response.
ax = mgr.showFit()
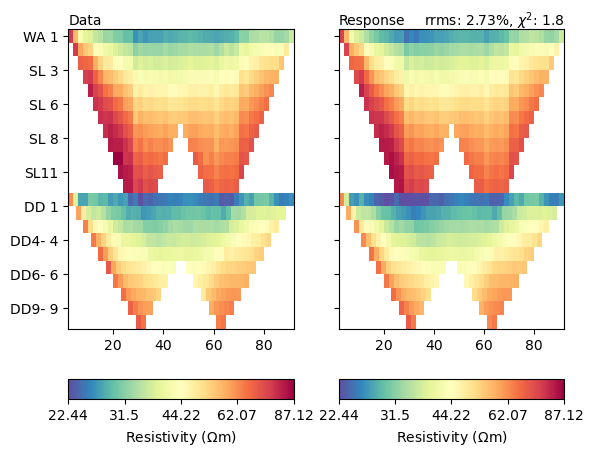
Both look very similar, but let us look at the misfit function in detail.
mgr.showMisfit(errorWeighted=True)
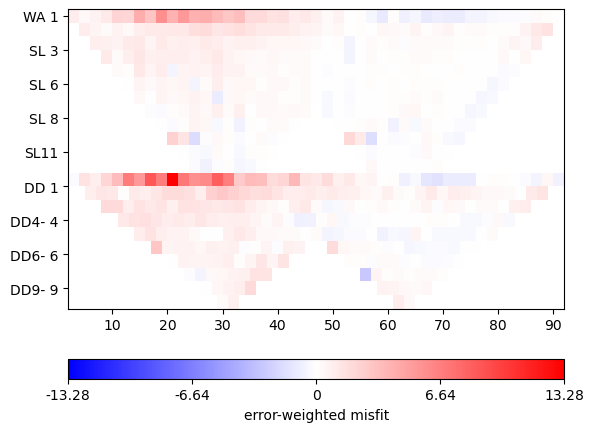
There is still systematics in the misfit. Ideally it should be a random distribution of Gaussian noise.
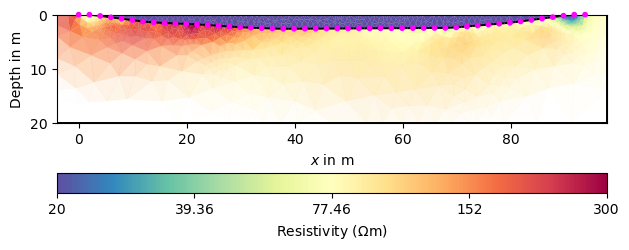
Apparently, the two regions are already decoupled from each other which makes sense. Let us look in detail at the water cells by extracting the water body. Note. The manager class performs a model value permutation to fit the parametric mesh cell. So if you want to relate model values to the input mesh, you need to use the unpermutated model values directly from the inversion framework instance: mgr.fw.model`
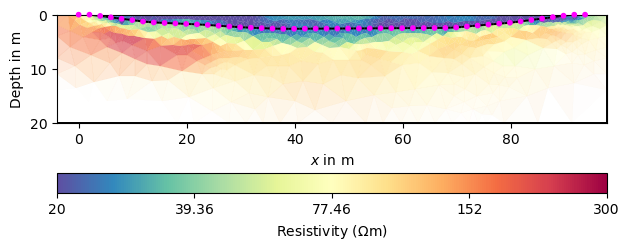
Apparently, all values are below the expected 22.5 :math:`Omega`m and some are implausibly low. Therefore we should try to limit them. Moreover, the subsurface structures do not look very “layered”, which is why we make the smoothness anisotropic.
fop: <pygimli.physics.ert.ertModelling.ERTModelling object at 0x1731e7d30>
Data transformation: Logarithmic LU transform, lower bound 0.0, upper bound 0.0
Model transformation (cumulative):
0 Logarithmic LU transform, lower bound 0.0, upper bound 0.0
1 Logarithmic LU transform, lower bound 0.0, upper bound 0.0
min/max (data): 22.44/87.12
min/max (error): 2%/2.58%
min/max (start model): 47.2/47.2
--------------------------------------------------------------------------------
inv.iter 0 ... chi² = 211.20
--------------------------------------------------------------------------------
inv.iter 1 ... chi² = 54.11 (dPhi = 74.35%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 2 ... chi² = 19.91 (dPhi = 63.15%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 3 ... chi² = 5.52 (dPhi = 72.04%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 4 ... chi² = 2.42 (dPhi = 55.55%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 5 ... chi² = 0.74 (dPhi = 67.51%) lam: 20.0
################################################################################
# Abort criterion reached: chi² <= 1 (0.74) #
################################################################################
Region-specific regularization#
We first want to limit the resistivity of the water between some plausible bounds around our measurements.
fop: <pygimli.physics.ert.ertModelling.ERTModelling object at 0x1731e7d30>
Data transformation: Logarithmic LU transform, lower bound 0.0, upper bound 0.0
Model transformation (cumulative):
0 Logarithmic LU transform, lower bound 0.0, upper bound 0.0
1 Logarithmic LU transform, lower bound 20.0, upper bound 25.0
min/max (data): 22.44/87.12
min/max (error): 2%/2.58%
min/max (start model): 47.2/47.2
--------------------------------------------------------------------------------
inv.iter 0 ... chi² = 211.20
--------------------------------------------------------------------------------
inv.iter 1 ... chi² = 65.56 (dPhi = 68.92%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 2 ... chi² = 24.14 (dPhi = 63.03%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 3 ... chi² = 3.32 (dPhi = 85.84%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 4 ... chi² = 0.47 (dPhi = 82.99%) lam: 20.0
################################################################################
# Abort criterion reached: chi² <= 1 (0.47) #
################################################################################
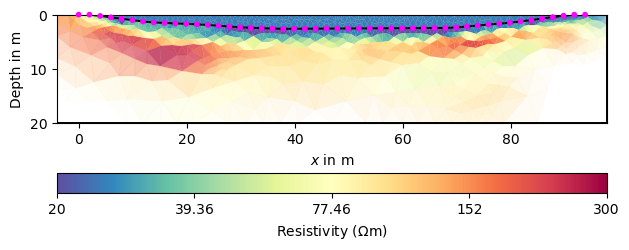
As a result of the log-log transform, we have a homogeneous body but below the lake bottom values below 20, maybe due to clay content or maybe as compensation of limiting the water resistivity too strong. We could limit the subsurface, too.
fop: <pygimli.physics.ert.ertModelling.ERTModelling object at 0x1731e7d30>
Data transformation: Logarithmic LU transform, lower bound 0.0, upper bound 0.0
Model transformation (cumulative):
0 Logarithmic LU transform, lower bound 20.0, upper bound 2000.0
1 Logarithmic LU transform, lower bound 20.0, upper bound 25.0
min/max (data): 22.44/87.12
min/max (error): 2%/2.58%
min/max (start model): 47.2/47.2
--------------------------------------------------------------------------------
inv.iter 0 ... chi² = 211.20
--------------------------------------------------------------------------------
inv.iter 1 ... chi² = 43.39 (dPhi = 79.21%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 2 ... chi² = 24.17 (dPhi = 43.41%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 3 ... chi² = 2.57 (dPhi = 87.85%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 4 ... chi² = 0.84 (dPhi = 59.96%) lam: 20.0
################################################################################
# Abort criterion reached: chi² <= 1 (0.84) #
################################################################################
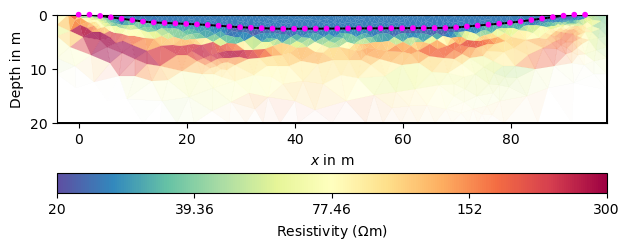
Apparently, this makes it harder to fit the data accurately. So maybe an increased clay content can be responsible for resistivity below 20:math:`Omega`m in the mud.
Model reduction#
Another option is to treat the water body as a homogeneous body with only one unknown in the inversion.
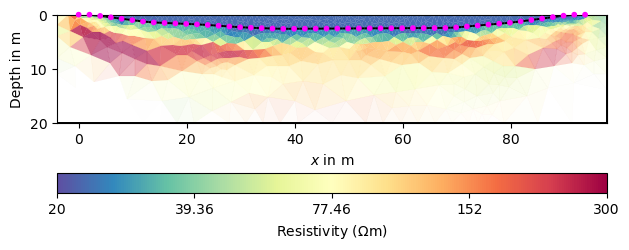
fop: <pygimli.physics.ert.ertModelling.ERTModelling object at 0x1731e7d30>
Data transformation: Logarithmic LU transform, lower bound 0.0, upper bound 0.0
Model transformation (cumulative):
0 Logarithmic LU transform, lower bound 20.0, upper bound 2000.0
1 Logarithmic LU transform, lower bound 20.0, upper bound 25.0
min/max (data): 22.44/87.12
min/max (error): 2%/2.58%
min/max (start model): 47.2/47.2
--------------------------------------------------------------------------------
inv.iter 0 ... chi² = 211.20
--------------------------------------------------------------------------------
inv.iter 1 ... chi² = 42.96 (dPhi = 80.01%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 2 ... chi² = 25.11 (dPhi = 41.20%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 3 ... chi² = 3.13 (dPhi = 86.20%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 4 ... chi² = 0.98 (dPhi = 63.14%) lam: 20.0
################################################################################
# Abort criterion reached: chi² <= 1 (0.98) #
################################################################################
The last value represents the value for the lake, close to our measurement. This value can, however, also be set beforehand.
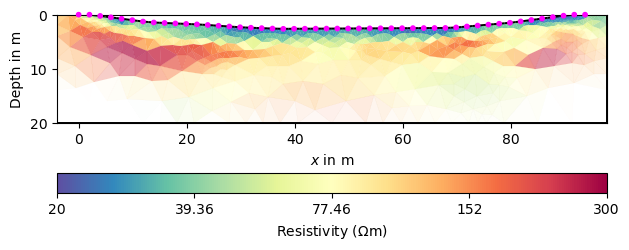
fop: <pygimli.physics.ert.ertModelling.ERTModelling object at 0x1731e7d30>
Data transformation: Logarithmic LU transform, lower bound 0.0, upper bound 0.0
Model transformation (cumulative):
0 Logarithmic LU transform, lower bound 20.0, upper bound 2000.0
min/max (data): 22.44/87.12
min/max (error): 2%/2.58%
min/max (start model): 47.2/47.2
--------------------------------------------------------------------------------
inv.iter 0 ... chi² = 145.34
--------------------------------------------------------------------------------
inv.iter 1 ... chi² = 29.66 (dPhi = 79.47%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 2 ... chi² = 19.21 (dPhi = 34.55%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 3 ... chi² = 2.31 (dPhi = 86.99%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 4 ... chi² = 0.96 (dPhi = 53.11%) lam: 20.0
################################################################################
# Abort criterion reached: chi² <= 1 (0.96) #
################################################################################
We see that the lake does not appear anymore as it is not a part of the
inversion mesh mgr.paraDomain anymore.
Instead of the standard smoothness we use geostatistical regularization.
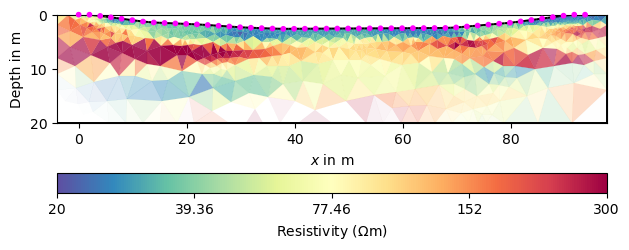
fop: <pygimli.physics.ert.ertModelling.ERTModelling object at 0x1731e7d30>
Data transformation: Logarithmic LU transform, lower bound 0.0, upper bound 0.0
Model transformation (cumulative):
0 Logarithmic LU transform, lower bound 20.0, upper bound 2000.0
min/max (data): 22.44/87.12
min/max (error): 2%/2.58%
min/max (start model): 47.2/47.2
--------------------------------------------------------------------------------
inv.iter 0 ... chi² = 145.34
--------------------------------------------------------------------------------
inv.iter 1 ... chi² = 21.41 (dPhi = 85.15%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 2 ... chi² = 9.30 (dPhi = 55.50%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 3 ... chi² = 1.79 (dPhi = 78.94%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 4 ... chi² = 0.99 (dPhi = 40.05%) lam: 20.0
################################################################################
# Abort criterion reached: chi² <= 1 (0.99) #
################################################################################
Region coupling#
In case (does not make sense here) the two regions should be coupled to each other, you can set so-called inter-region constraints.
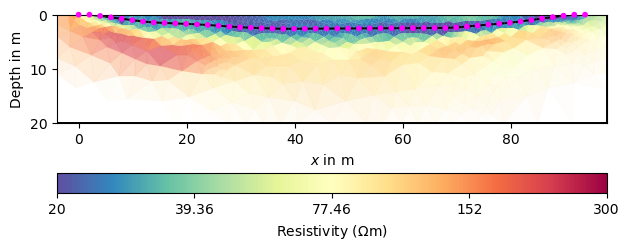
Number of regions: 3
fop: <pygimli.physics.ert.ertModelling.ERTModelling object at 0x323be4360>
Data transformation: Logarithmic LU transform, lower bound 0.0, upper bound 0.0
Model transformation (cumulative):
0 Logarithmic LU transform, lower bound 0.0, upper bound 0.0
1 Logarithmic LU transform, lower bound 0.0, upper bound 0.0
min/max (data): 22.44/87.12
min/max (error): 2%/2.58%
min/max (start model): 47.2/47.2
--------------------------------------------------------------------------------
inv.iter 0 ... chi² = 211.20
--------------------------------------------------------------------------------
inv.iter 1 ... chi² = 37.59 (dPhi = 82.12%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 2 ... chi² = 17.29 (dPhi = 53.85%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 3 ... chi² = 3.64 (dPhi = 78.28%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 4 ... chi² = 1.47 (dPhi = 56.98%) lam: 20.0
--------------------------------------------------------------------------------
inv.iter 5 ... chi² = 0.40 (dPhi = 65.59%) lam: 20.0
################################################################################
# Abort criterion reached: chi² <= 1 (0.40) #
################################################################################
The general image is of course similar, but the structures are mirrored around the lake bottom. Moreover the resistivity in the lake is far too high. Note that all of the obtained images are equivalent with respect to data and errors.
Take-away messages#
always have a look at the data fit and get hands on data errors
a lot of different models are able to fit the data, particularly in the full space
regions can be very specifically controlled
constrain or fix whenever possibly (and reliable)
sometimes geostatistic constraints outperform classical smoothness but sometimes not
play with regularization and keep looking at data fit
Total running time of the script: (0 minutes 57.881 seconds)