pygimli.utils

Useful utility functions.

Overview

Functions

GKtoUTM(ea[, no, zone, gk, gkzone])	Transform any Gauss-Krueger to UTM autodetect GK zone from offset.
KramersKronig(f, re, im[, usezero])	Return real/imaginary parts retrieved by Kramers-Kronig relations.
boxprint(s[, width, sym])	Print string centered in a box.
cMap(name)	Return default colormap for physical quantity name.
cache(funct)	Cache decorator.
chi2(a, b, err[, trans])	Return chi square value.
cmap(name)	Return default colormap for physical quantity name.
computeInverseRootMatrix(CM[, thrsh, verbose])	Compute inverse square root (C^{-0.5} of matrix.
convertCRSIndex2Map(rowIdx, colPtr)	Converts CRS indices to uncompressed indices (row, col).
covarianceMatrix(mesh[, nodes])	Geostatistical covariance matrix (cell or node) for given mesh.
createDateTimeString([now])	Return datetime as string (e.g.
createFolders(*args, **kwargs)
createPath(pathList)	Create the path structure specified by list.
createResultFolder(*args, **kwargs)
createResultPath(subfolder[, now])	Create a result Folder.
createfolders(*args, **kwargs)
cumDist(p)	The progressive, i.e., cumulative length for a path p.
cut(v[, n])	Cut array v into n parts.
diff(v)	Calculate approximate derivative.
dist(p[, c])	Calculate the distance for each position in p relative to pos c(x,y,z).
filterIndex(seq, idx)	TODO DOCUMENTME.
filterLinesByCommentStr(lines[, comment_str])	Filter lines from file.readlines() beginning with symbols in comment.
findNearest(x, y, xp, yp[, radius])	TODO DOCUMENTME.
findUTMZone(lon, lat)	Find utm zone for lon and lat values.
generateGeostatisticalModel(mesh[, nodes, seed])	Generate geostatistical model (cell or node) for given mesh.
getIndex(seq, f)	TODO DOCUMENTME.
getProjection(name[, ref])	Syntactic sugar to get some default Projections.
getSavePath([folder, subfolder, now])	TODO.
getUTMProjection(zone[, ellps])	Create and return the current coordinate projection.
gmat2numpy(mat)	Convert pygimli matrix into numpy.array.
grange(start, end[, dx, n, log])	Create array with possible increasing spacing.
hankelFC(order)	Filter coefficients for Hankel transformation.
interpExtrap(x, xp, yp)	numpy.interp interpolation function extended by linear extrapolation.
interperc(a[, trimval, islog, bins])	Return symmetric interpercentiles for alpha-trim outliers.
inthist(a, vals[, bins, islog])	Return point of integral (cumulative) histogram.
isComplex(vals)	Check numpy or pg.Vector if have complex data type
iterateBounds(inv[, dchi2, maxiter, change])	Find parameter bounds by iterating model parameter.
logDropTol(p[, dropTol])	Create logarithmic scaled copy of p.
modCovar(inv)	Formal model covariance matrix (MCM) from inversion.
nanrms(v[, axis])	Compute the root mean square excluding nan values.
niceLogspace(vMin, vMax[, nDec])	Nice logarithmic space from decade < vMin to decade > vMax.
noCache(c)
num2str(a[, fmtstr])	List of strings (deprecated, for backward-compatibility).
numpy2gmat(nmat)	Convert numpy.array into pygimli RMatrix.
prettify(value[, roundValue])	Return prettified string for value .
prettyFloat(value[, roundValue])	Return prettified string for a float value.
prettyTime(t)	Return prettified time in seconds as string.
rand(n[, minVal, maxVal, seed])	Create RVector of length n with normally distributed random numbers.
randn(n[, seed])	Create n normally distributed random numbers with optional seed.
readGPX(fileName)	Extract GPS Waypoint from GPS Exchange Format (GPX).
rms(v[, axis])	Compute the root mean square.
rmsWithErr(a, b, err[, errtol])	Compute (abs-)root-mean-square of values with error above threshold.
rmswitherr(a, b, err[, errtol])	Compute (abs-)root-mean-square of values with error above threshold.
rndig(a[, ndig])	Round float using a number of counting digits.
rrms(a, b[, axis])	Compute the relative (regarding a) root mean square.
saveResult(fname, data[, rrms, chi2, mode])	Save rms/chi2 results into filename.
sparseMatrix2Array(matrix[, indices, getInCRS])	Extract indices and value from sparse matrix (SparseMap or CRS)
sparseMatrix2Dense(matrix)	Convert sparse matrix to dense ndarray
sparseMatrix2coo(A[, rowOffset, colOffset])	Convert SparseMatrix to scipy.coo_matrix.
sparseMatrix2csr(A)	Convert SparseMatrix to scipy.csr_matrix.
squeezeComplex(z[, polar, conj])	Squeeze complex valued array into [real, imag] or [amp, phase(rad)]
strHash(string)
streamline(mesh, field, startCoord, dLengthSteps)	Create a streamline from start coordinate and following a vector field in up and down direction.
streamlineDir(mesh, field, startCoord, ...)	down = -1, up = 1, both = 0
toCOO(A)
toCSR(A)
toComplex(amp[, phi])	Convert real values into complex (z = a + ib) valued array.
toPolar(z)	Convert complex (z = a + ib) values array into amplitude and phase in radiant
toRealMatrix(C[, conj])	Convert complex valued matrix into a real valued Blockmatrix
toSparseMapMatrix(A)	Convert any matrix type to pg.SparseMatrix and return copy of it.
toSparseMatrix(A)	Convert any matrix type to pg.SparseMatrix and return copy of it.
trimDocString(docstring)	Return properly formatted docstring.
unicodeToAscii(text)	TODO DOCUMENTME.
unique(a)	Return list of unique elements ever seen with preserving order.
uniqueAndSum(indices, to_sum[, ...])	Sum double values found by indices in a various number of arrays.
unique_everseen(iterable[, key])	Return iterator of unique elements ever seen with preserving order.
unique_rows(array)	Return unique rows in a 2D array.
unit(name[, unit])	Return the name of a physical quantity with its unit.

Classes

ProgressBar(its[, width, sign])

Animated text-based progress bar.

Functions

pygimli.utils.GKtoUTM(ea, no=None, zone=32, gk=None, gkzone=None)

Transform any Gauss-Krueger to UTM autodetect GK zone from offset.

pygimli.utils.KramersKronig(f, re, im, usezero=False)

Return real/imaginary parts retrieved by Kramers-Kronig relations.

formulas including singularity removal according to Boukamp (1993)

pygimli.utils.boxprint(s, width=80, sym='#')

Print string centered in a box.

Examples

>>> from pygimli.utils import boxprint
>>> boxprint("This is centered in a box.", width=40, sym='+')
++++++++++++++++++++++++++++++++++++++++
+      This is centered in a box.      +
++++++++++++++++++++++++++++++++++++++++

pygimli.utils.cMap(name)

Return default colormap for physical quantity name.

pygimli.utils.cache(funct)

Cache decorator.

pygimli.utils.chi2(a, b, err, trans=None)

Return chi square value.

pygimli.utils.cmap(name)

Return default colormap for physical quantity name.

pygimli.utils.computeInverseRootMatrix(CM, thrsh=0.001, verbose=False)

Compute inverse square root (C^{-0.5} of matrix.

pygimli.utils.convertCRSIndex2Map(rowIdx, colPtr)

Converts CRS indices to uncompressed indices (row, col).

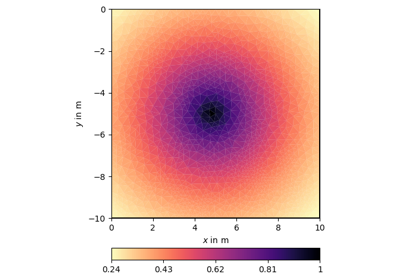
pygimli.utils.covarianceMatrix(mesh, nodes=False, **kwargs)

Geostatistical covariance matrix (cell or node) for given mesh.

Parameters

• mesh (gimliapi:GIMLI::Mesh) – Mesh

• nodes (bool [False]) – use node positions, otherwise (default) cell centers are used

• **kwargs –

  Ifloat or list of floats

  correlation lengths (range) in individual directions

  dipfloat

  dip angle (in degree) of major axis (I[0])

  strikefloat

  strike angle (for 3D)

Returns

Cm – covariance matrix

Return type

np.array (square matrix of size cellCount/nodeCount)

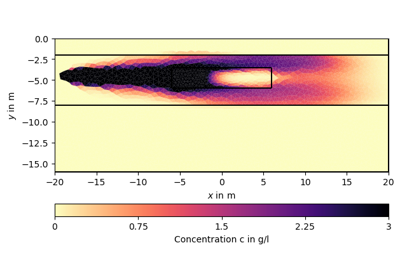
Examples using pygimli.utils.covarianceMatrix

Geostatistical regularization

Geostatistical regularization

pygimli.utils.createDateTimeString(now=None)

Return datetime as string (e.g. for saving results).

pygimli.utils.createFolders(*args, **kwargs)

pygimli.utils.createPath(pathList)

Create the path structure specified by list.

Parameters

pathList (str | list(str)) – Create Path with option subpaths

pygimli.utils.createResultFolder(*args, **kwargs)

pygimli.utils.createResultPath(subfolder, now=None)

Create a result Folder.

pygimli.utils.createfolders(*args, **kwargs)

pygimli.utils.cumDist(p)

The progressive, i.e., cumulative length for a path p.

d = [0.0, d[0]+ | p[1]-p[0] |, d[1] + | p[2]-p[1] | + …]

Parameters

p (ndarray(N,2) | ndarray(N,3) | pg.PosVector) – Position array

Returns

d – Distance array

Return type

ndarray(N)

Examples

>>> import pygimli as pg
>>> from pygimli.utils import cumDist
>>> import numpy as np
>>> p = pg.PosVector(4)
>>> p[0] = [0.0, 0.0]
>>> p[1] = [0.0, 1.0]
>>> p[2] = [0.0, 1.0]
>>> p[3] = [0.0, 0.0]
>>> print(cumDist(p))
[0. 1. 1. 2.]

pygimli.utils.cut(v, n=2)

Cut array v into n parts.

pygimli.utils.diff(v)

Calculate approximate derivative.

Calculate approximate derivative from v as d = [v_1-v_0, v2-v_1, …]

Parameters

v (array(N) | pg.PosVector(N)) – Array of double values or positions

Returns

d – derivative array

Return type

[type(v)](N-1) |

Examples

>>> import pygimli as pg
>>> from pygimli.utils import diff
>>> p = pg.PosVector(4)
>>> p[0] = [0.0, 0.0]
>>> p[1] = [0.0, 1.0]
>>> print(diff(p)[0])
RVector3: (0.0, 1.0, 0.0)
>>> print(diff(p)[1])
RVector3: (0.0, -1.0, 0.0)
>>> print(diff(p)[2])
RVector3: (0.0, 0.0, 0.0)
>>> p = pg.Vector(3)
>>> p[0] = 0.0
>>> p[1] = 1.0
>>> p[2] = 2.0
>>> print(diff(p))
2 [1.0, 1.0]

pygimli.utils.dist(p, c=None)

Calculate the distance for each position in p relative to pos c(x,y,z).

Parameters

• p (ndarray(N,2) | ndarray(N,3) | pg.PosVector) – Position array

• c ([x,y,z] [None]) – relative origin. default = [0, 0, 0]

Returns

d – Distance array

Return type

ndarray(N)

Examples

>>> import pygimli as pg
>>> from pygimli.utils import dist
>>> import numpy as np
>>> p = pg.PosVector(4)
>>> p[0] = [0.0, 0.0]
>>> p[1] = [0.0, 1.0]
>>> print(dist(p))
[0. 1. 0. 0.]
>>> x = pg.Vector(4, 0)
>>> y = pg.Vector(4, 1)
>>> print(dist(np.array([x, y]).T))
[1. 1. 1. 1.]

pygimli.utils.filterIndex(seq, idx)

TODO DOCUMENTME.

pygimli.utils.filterLinesByCommentStr(lines, comment_str='#')

Filter lines from file.readlines() beginning with symbols in comment.

pygimli.utils.findNearest(x, y, xp, yp, radius=-1)

TODO DOCUMENTME.

pygimli.utils.findUTMZone(lon, lat)

Find utm zone for lon and lat values.

lon -180 – -174 -> 1 … 174 – 180 -> 60 lat < 0 hemisphere = S, > 0 hemisphere = N

Parameters

• lon (float) –

• lat (float) –

Returns

zone + hemisphere

Return type

str

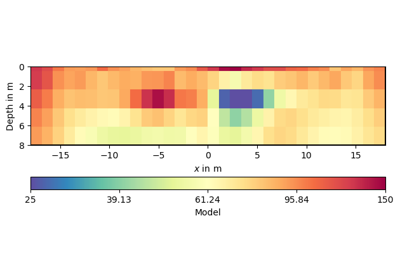
pygimli.utils.generateGeostatisticalModel(mesh, nodes=False, seed=None, **kwargs)

Generate geostatistical model (cell or node) for given mesh.

Parameters

• mesh (gimliapi:GIMLI::Mesh) – Mesh

• nodes (bool [False]) – use node positions, otherwise (default) cell centers are used

• seed (int, array_like[ints], SeedSequence, BitGenerator, Generator}, optional) – A seed to initialize the BitGenerator. If None, then fresh, unpredictable entropy will be used. The seed variable is passed to numpy.random.default_rng()

• **kwargs –

  Ifloat or list of floats

  correlation lengths (range) in individual directions

  dipfloat

  dip angle of major axis (I[0])

  strikefloat

  strike angle (for 3D)

Returns

res

Return type

np.array of size cellCount or nodeCount (nodes=True)

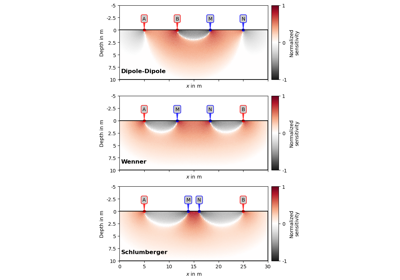
Examples using pygimli.utils.generateGeostatisticalModel

Geostatistical regularization

Geostatistical regularization

pygimli.utils.getIndex(seq, f)

TODO DOCUMENTME.

pygimli.utils.getProjection(name, ref=None, **kwargs)

Syntactic sugar to get some default Projections.

pygimli.utils.getSavePath(folder=None, subfolder='', now=None)

TODO.

pygimli.utils.getUTMProjection(zone, ellps='WGS84')

Create and return the current coordinate projection.

This is a proxy for pyproj.

Parameters

• utmZone (str) – Zone for for UTM

• ellipsoid (str) – ellipsoid based on [‘wgs84’]

Return type

Pyproj Projection

pygimli.utils.gmat2numpy(mat)

Convert pygimli matrix into numpy.array.

TODO implement correct rval

pygimli.utils.grange(start, end, dx=0, n=0, log=False)

Create array with possible increasing spacing.

Create either array from start step-wise filled with dx until end reached [start, end] (like np.array with defined end). Fill the array from start to end with n steps. [start, end] (like np.linespace) Fill the array from start to end with n steps but logarithmic increasing, dx will be ignored.

Parameters

• start (float) – First value of the resulting array

• end (float) – Last value of the resulting array

• dx (float) – Linear step length, n will be ignored

• n (int) – Amount of steps

• log (bool) – Logarithmic increasing range of length = n from start to end. dx will be ignored.

Examples

>>> from pygimli.utils import grange
>>> v1 = grange(start=0, end=10, dx=3)
>>> v2 = grange(start=0, end=10, n=3)
>>> print(v1)
4 [0.0, 3.0, 6.0, 9.0]
>>> print(v2)
3 [0.0, 5.0, 10.0]

Returns

ret – Return resulting array

Return type

GIMLI::RVector

Examples using pygimli.utils.grange

2D ERT modeling and inversion

2D ERT modeling and inversion

2D FEM modelling on two-layer example

2D FEM modelling on two-layer example

Hydrogeophysical modeling

Hydrogeophysical modeling

pygimli.utils.hankelFC(order)

Filter coefficients for Hankel transformation.

10 data points per decade.

DOCUMENTME .. Author RUB?

Parameters

order (int) – order=1: NY=+0.5 (SIN) order=2: NY=-0.5 (COS) order=3: NY=0.0 (J0) order=4: NY=1.0 (J1)

Returns

• fc (np.array()) – Filter coefficients

• nc0 (int) – fc[nc0] refers to zero argument

pygimli.utils.interpExtrap(x, xp, yp)

numpy.interp interpolation function extended by linear extrapolation.

pygimli.utils.interperc(a, trimval=3.0, islog=False, bins=None)

Return symmetric interpercentiles for alpha-trim outliers.

E.g. interperc(a, 3) returns range of inner 94% (3 to 97%) which is particularly useful for colorscales).

pygimli.utils.inthist(a, vals, bins=None, islog=False)

Return point of integral (cumulative) histogram.

E.g. inthist(a, [25, 50, 75]) provides quartiles and median of an array

pygimli.utils.isComplex(vals)

Check numpy or pg.Vector if have complex data type

pygimli.utils.iterateBounds(inv, dchi2=0.5, maxiter=100, change=1.02)

Find parameter bounds by iterating model parameter.

Find parameter bounds by iterating model parameter until error bound is reached

Parameters

• inv – gimli inversion object

• dchi2 – allowed variation of chi^2 values [0.5]

• maxiter – maximum iteration number for parameter iteration [100]

• change – changing factor of parameters [1.02, i.e. 2%]

pygimli.utils.logDropTol(p, dropTol=0.001)

Create logarithmic scaled copy of p.

Examples

>>> from pygimli.utils import logDropTol
>>> x = logDropTol((-10, -1, 0, 1, 100))
>>> print(x.array())
[-4. -3.  0.  3.  5.]

Examples using pygimli.utils.logDropTol

Four-point sensitivities

Four-point sensitivities

pygimli.utils.modCovar(inv)

Formal model covariance matrix (MCM) from inversion.

var, MCMs = modCovar(inv)

Parameters

inv (pygimli inversion object) –

Returns

• var (variances (inverse square roots of MCM matrix))

• MCMs (scaled MCM (such that diagonals are 1.0))

>>> # import pygimli as pg
>>> # import matplotlib.pyplot as plt
>>> # from matplotlib.cm import bwr
>>> # INV = pg.Inversion(data, f)
>>> # par = INV.run()
>>> # var, MCM = modCovar(INV)
>>> # i = plt.imshow(MCM, interpolation='nearest',
>>> #                 cmap=bwr, vmin=-1, vmax=1)
>>> # plt.colorbar(i)

pygimli.utils.nanrms(v, axis=None)

Compute the root mean square excluding nan values.

pygimli.utils.niceLogspace(vMin, vMax, nDec=10)

Nice logarithmic space from decade < vMin to decade > vMax.

Parameters

• vMin (float) – lower limit need to be > 0

• vMax (float) – upper limit need to be >= vMin

• nDec (int) – Amount of logarithmic equidistant steps for one decade

Examples

>>> from pygimli.utils import niceLogspace
>>> v1 = niceLogspace(vMin=0.1, vMax=0.1, nDec=1)
>>> print(v1)
[0.1 1. ]
>>> v1 = niceLogspace(vMin=0.09, vMax=0.11, nDec=1)
>>> print(v1)
[0.01 0.1  1.  ]
>>> v1 = niceLogspace(vMin=0.09, vMax=0.11, nDec=10)
>>> print(len(v1))
21
>>> print(v1)
[0.01       0.01258925 0.01584893 0.01995262 0.02511886 0.03162278
 0.03981072 0.05011872 0.06309573 0.07943282 0.1        0.12589254
 0.15848932 0.19952623 0.25118864 0.31622777 0.39810717 0.50118723
 0.63095734 0.79432823 1.        ]

pygimli.utils.noCache(c)

pygimli.utils.num2str(a, fmtstr='%g')

List of strings (deprecated, for backward-compatibility).

pygimli.utils.numpy2gmat(nmat)

Convert numpy.array into pygimli RMatrix.

TODO implement correct rval

pygimli.utils.prettify(value, roundValue=False)

Return prettified string for value .. if possible.

pygimli.utils.prettyFloat(value, roundValue=None)

Return prettified string for a float value.

pygimli.utils.prettyTime(t)

Return prettified time in seconds as string. No months, no leap year.

Parameters

t (float) – Time in seconds, should be > 0

Examples

>>> from pygimli.utils import prettyTime
>>> print(prettyTime(1))
1 s
>>> print(prettyTime(3600*24))
1 day
>>> print(prettyTime(2*3600*24))
2 days
>>> print(prettyTime(365*3600*24))
1 year
>>> print(prettyTime(3600))
1 hour
>>> print(prettyTime(2*3600))
2 hours
>>> print(prettyTime(3660))
1h1m
>>> print(prettyTime(1e-3))
1 ms
>>> print(prettyTime(1e-6))
1 µs
>>> print(prettyTime(1e-9))
1 ns

pygimli.utils.rand(n, minVal=0.0, maxVal=1.0, seed=None)

Create RVector of length n with normally distributed random numbers.

pygimli.utils.randn(n, seed=None)

Create n normally distributed random numbers with optional seed.

Parameters

• n (long) – length of random numbers array.

• seed (int[None]) – Optional seed for random number generator

Returns

r – Random numbers.

Return type

np.array

Examples

>>> import numpy as np
>>> from pygimli.utils import randn
>>> a = randn(5, seed=1337)
>>> b = randn(5)
>>> c = randn(5, seed=1337)
>>> print(np.array_equal(a, b))
False
>>> print(np.array_equal(a, c))
True

pygimli.utils.readGPX(fileName)

Extract GPS Waypoint from GPS Exchange Format (GPX).

Currently only simple waypoint extraction is supported.

<gpx version=”1.0” creator=”creator”>

<metadata> <name>Name</name> </metadata> <wpt lat=”51.” lon=”11.”> <name>optional</name> <time>optional</time> <description>optional</description> </wpt>

</gpx>

pygimli.utils.rms(v, axis=None)

Compute the root mean square.

pygimli.utils.rmsWithErr(a, b, err, errtol=1)

Compute (abs-)root-mean-square of values with error above threshold.

pygimli.utils.rmswitherr(a, b, err, errtol=1)

Compute (abs-)root-mean-square of values with error above threshold.

pygimli.utils.rndig(a, ndig=3)

Round float using a number of counting digits.

pygimli.utils.rrms(a, b, axis=None)

Compute the relative (regarding a) root mean square.

pygimli.utils.saveResult(fname, data, rrms=None, chi2=None, mode='w')

Save rms/chi2 results into filename.

pygimli.utils.sparseMatrix2Array(matrix, indices=True, getInCRS=True)

Extract indices and value from sparse matrix (SparseMap or CRS)

Get python Arrays from SparseMatrix or SparseMapMatrix in either CRS convention (row index, column Start_End, values) or row index, column index, values.

Parameters

• matrix (pg.matrix.SparseMapMatrix or pg.matrix.SparseMatrix) – Input matrix to be transformed to numpy arrays.

• indices (boolean (True)) – Decides weather the indices of the matrix will be returned or not.

• getInCSR (boolean (True)) – If returned, the indices can have the format of a compressed row storage (CSR), the default or uncompressed lists with column and row indices.

Returns

• vals (numpy.ndarray) – Entries of the matrix.

• indices (list, list) – Optional. Returns additional array with the indices for reconstructing the matrix in the defined format.

pygimli.utils.sparseMatrix2Dense(matrix)

Convert sparse matrix to dense ndarray

pygimli.utils.sparseMatrix2coo(A, rowOffset=0, colOffset=0)

Convert SparseMatrix to scipy.coo_matrix.

Parameters

A (pg.matrix.SparseMapMatrix | pg.matrix.SparseMatrix) – Matrix to convert from.

Returns

mat – Matrix to convert into.

Return type

scipy.coo_matrix

Examples using pygimli.utils.sparseMatrix2coo

Naive complex-valued electrical inversion

Naive complex-valued electrical inversion

pygimli.utils.sparseMatrix2csr(A)

Convert SparseMatrix to scipy.csr_matrix.

Compressed Sparse Row matrix, i.e., Compressed Row Storage (CRS)

Parameters

A (pg.matrix.SparseMapMatrix | pg.matrix.SparseMatrix) – Matrix to convert from.

Returns

mat – Matrix to convert into.

Return type

scipy.csr_matrix

pygimli.utils.squeezeComplex(z, polar=False, conj=False)

Squeeze complex valued array into [real, imag] or [amp, phase(rad)]

Examples using pygimli.utils.squeezeComplex

Naive complex-valued electrical inversion

Naive complex-valued electrical inversion

pygimli.utils.strHash(string)

pygimli.utils.streamline(mesh, field, startCoord, dLengthSteps, dataMesh=None, maxSteps=1000, verbose=False, coords=(0, 1))

Create a streamline from start coordinate and following a vector field in up and down direction.

pygimli.utils.streamlineDir(mesh, field, startCoord, dLengthSteps, dataMesh=None, maxSteps=150, down=True, verbose=False, coords=(0, 1))

down = -1, up = 1, both = 0

pygimli.utils.toCOO(A)

pygimli.utils.toCSR(A)

pygimli.utils.toComplex(amp, phi=None)

Convert real values into complex (z = a + ib) valued array.

If no phases phi are given, assuming z = amp[0:N] + i amp[N:2N].

If phi is given in (rad) complex values are generated: z = amp*(cos(phi) + i sin(phi))

Parameters

• amp (iterable (float)) – Amplitudes or real unsqueezed real valued array.

• phi (iterable (float)) – Phases in neg radiant

Returns

z – Complex values

Return type

ndarray(dtype=np.complex)

Examples using pygimli.utils.toComplex

Complex-valued electrical modeling

Complex-valued electrical modeling

Naive complex-valued electrical inversion

Naive complex-valued electrical inversion

pygimli.utils.toPolar(z)

Convert complex (z = a + ib) values array into amplitude and phase in radiant

If z is real valued we assume its squeezed.

Parameters

z (iterable (floats, complex)) – If z contains of floats and squeezedComplex is assumed [real, imag]

Returns

amp, phi – Amplitude amp and phase angle phi in radiant.

Return type

ndarray

pygimli.utils.toRealMatrix(C, conj=False)

Convert complex valued matrix into a real valued Blockmatrix

Parameters

• C (CMatrix) – Complex valued matrix

• conj (bool [False]) – Fill the matrix as complex conjugated matrix

Returns

R

Return type

pg.matrix.BlockMatrix()

pygimli.utils.toSparseMapMatrix(A)

Convert any matrix type to pg.SparseMatrix and return copy of it.

Parameters

A (pg or scipy matrix) –

Return type

pg.SparseMatrix

pygimli.utils.toSparseMatrix(A)

Convert any matrix type to pg.SparseMatrix and return copy of it.

No conversion if A is a SparseMatrix already :param A: :type A: pg or scipy matrix

Return type

pg.SparseMatrix

pygimli.utils.trimDocString(docstring)

Return properly formatted docstring.

From: https://www.python.org/dev/peps/pep-0257/

Examples

>>> from pygimli.utils import trimDocString
>>> docstring = '    This is a string with indention and whitespace.   '
>>> trimDocString(docstring).replace('with', 'without')
'This is a string without indention and whitespace.'

pygimli.utils.unicodeToAscii(text)

TODO DOCUMENTME.

pygimli.utils.unique(a)

Return list of unique elements ever seen with preserving order.

Examples

>>> from pygimli.utils import unique
>>> unique((1,1,2,2,3,1))
[1, 2, 3]

See also

unique_everseen, unique_rows

pygimli.utils.uniqueAndSum(indices, to_sum, return_index=False, verbose=False)

Sum double values found by indices in a various number of arrays.

Returns the sorted unique elements of a column_stacked array of indices. Another column_stacked array is returned with values at the unique indices, while values at double indices are properly summed.

Parameters

• ar (array_like) – Input array. This will be flattened if it is not already 1-D.

• to_sum (array_like) – Input array to be summed over axis 0. Other existing axes will be broadcasted remain untouched.

• return_index (bool, optional) – If True, also return the indices of ar (along the specified axis, if provided, or in the flattened array) that result in the unique array.

Returns

• unique (ndarray) – The sorted unique values.

• summed_array (ndarray) – The summed array, whereas all values for a specific index is the sum over all corresponding nonunique values.

• unique_indices (ndarray, optional) – The indices of the first occurrences of the unique values in the original array. Only provided if return_index is True.

Examples

>>> import numpy as np
>>> from pygimli.utils import uniqueAndSum
>>> idx1 = np.array([0, 0, 1, 1, 2, 2])
>>> idx2 = np.array([0, 0, 1, 2, 3, 3])
>>> # indices at positions 0 and 1 and at positions 5 and 6 are not unique
>>> to_sort = np.column_stack((idx1, idx2))
>>> # its possible to stack more than two array
>>> # you need for example 3 array to find unique node positions in a mesh
>>> values = np.arange(0.1, 0.7, 0.1)
>>> print(values)
[0.1 0.2 0.3 0.4 0.5 0.6]
>>> # some values to be summed together (for example attributes of nodes)
>>> unique_idx, summed_vals = uniqueAndSum(to_sort, values)
>>> print(unique_idx)
[[0 0]
 [1 1]
 [1 2]
 [2 3]]
>>> print(summed_vals)
[0.3 0.3 0.4 1.1]

pygimli.utils.unique_everseen(iterable, key=None)

Return iterator of unique elements ever seen with preserving order.

Return iterator of unique elements ever seen with preserving order.

From: https://docs.python.org/3/library/itertools.html#itertools-recipes

Examples

>>> from pygimli.utils import unique_everseen
>>> s1 = 'AAAABBBCCDAABBB'
>>> s2 = 'ABBCcAD'
>>> list(unique_everseen(s1))
['A', 'B', 'C', 'D']
>>> list(unique_everseen(s2, key=str.lower))
['A', 'B', 'C', 'D']

See also

unique, unique_rows

pygimli.utils.unique_rows(array)

Return unique rows in a 2D array.

Examples

>>> from pygimli.utils import unique_rows
>>> import numpy as np
>>> A = np.array(([1,2,3],[3,2,1],[1,2,3]))
>>> unique_rows(A)
array([[1, 2, 3],
       [3, 2, 1]])

pygimli.utils.unit(name, unit='auto')

Return the name of a physical quantity with its unit.

Classes

class pygimli.utils.ProgressBar(its, width=80, sign=':', **kwargs)

Bases: object

Animated text-based progress bar.

Animated text-based progressbar for intensive loops. Should work in the console. In IPython Notebooks a ‘tqdm’ progressbar instance is created and can be configured with appropriate keyword arguments.

__init__(its, width=80, sign=':', **kwargs)

Create animated text-based progress bar.

• optional: ‘estimated time’ instead of ‘x of y complete’

itsint

Number of iterations of the process.

widthint

Width of the ProgressBar, default is 80.

signstr

Sign used to fill the bar.

Forwarded to create the tqdm progressbar instance. See https://tqdm.github.io/docs/tqdm/

>>> from pygimli.utils import ProgressBar
>>> pBar = ProgressBar(its=20, width=40, sign='+')
>>> pBar.update(5)

[+++++++++++ 30% ] 6 of 20 complete

update(iteration, msg='')

Update by iteration number starting at 0 with optional message.