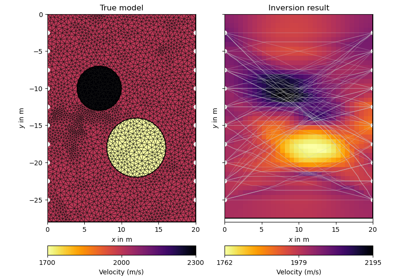
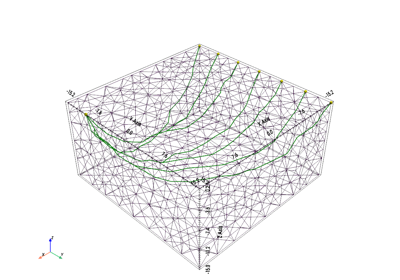
pygimli.physics.traveltime#

Refraction seismics or first arrival traveltime calculations.

Overview#

Functions

`createCrossholeData`([sensors, x, z])	Create crosshole scheme assuming two boreholes with equal sensor numbers.
`createGradientModel2D`(data, mesh, vTop, vBot)	Create 2D velocity gradient model.
`createRAData`(sensors[, shotDistance])	Create a refraction data container.
`drawFirstPicks`(ax, data[, tt, plotva])	Plot first arrivals as lines.
`drawTravelTimeData`(ax, data[, t])	Draw first arrival traveltime data into mpl ax a.
`drawVA`(ax, data[, vals, usePos, pseudosection])	Draw apparent velocities as matrix into an axis.
`load`(fileName[, verbose])	Shortcut to load TravelTime data.
`shotReceiverDistances`(data[, full])	Distance vector between shot and for each 's' and 'g' in data.
`show`(data, **kwargs)	Show data.
`showVA`(data[, usePos, ax])	Show apparent velocity as image plot.
`simulate`(mesh, scheme[, slowness])	Simulate traveltime measurements.

Classes

`DataContainer`	alias of `DataContainerTT`
`DataContainerTT`([data])	Data Container for traveltime.
`Dijkstra`	Dijkstras shortest path finding
`Manager`	alias of `TravelTimeManager`
`RefractionNLayer`([offset, nlay, vbase, verbose])	Forward operator for 1D Refraction seismic with layered model.
`RefractionNLayerFix1stLayer`([offset, nlay, ...])	FOP for 1D Refraction seismic with layered model (e.g. water layer).
`TravelTimeDijkstraModelling`(**kwargs)	Forward modelling class for traveltime using Dijktras method.
`TravelTimeManager`([data])	Manager for refraction seismics (traveltime tomography).
`TravelTimeModelling`	alias of `TravelTimeDijkstraModelling`

Functions#

pygimli.physics.traveltime.createCrossholeData(sensors=None, x=None, z=None)[source]#

Create crosshole scheme assuming two boreholes with equal sensor numbers.

Parameters:

sensors (array (Nx2)) – Array with position of sensors. Alternatively, specify x and z
x (iterable [M]) – horizontal positions of boreholes
z (iterable [M]) – vertical positions of sensors in each borehole

Returns:

scheme – Data container with sensors predefined sensor indices ‘s’ and ‘g’ for shot and receiver numbers.

Return type:

DataContainer

Examples using pygimli.physics.traveltime.createCrossholeData

Crosshole traveltime tomography

pygimli.physics.traveltime.createGradientModel2D(data, mesh, vTop, vBot, flat=False)[source]#

Create 2D velocity gradient model.

Creates a smooth, linear, starting model that takes the slope of the topography into account. This is done by fitting a straight line and using the distance to that as the depth value.

Parameters:

data (pygimli DataContainer) – The topography list is in here.
mesh (pygimli.Mesh) – The parametric mesh used for the inversion
vTop (float) – The velocity at the surface of the mesh
vBot (float) – The velocity at the bottom of the mesh

Returns:

model – A numpy array with slowness values that can be used to start the inversion.

Return type:

pygimli Vector, length M

pygimli.physics.traveltime.createRAData(sensors, shotDistance=1)[source]#

Create a refraction data container.

Default data container for shot and geophon at every sensor position. Predefined sensor indices’s ‘s’ as shot position and ‘g’ as geophon position.

Parameters:

sensors (ndarray | R3Vector) – Geophon and shot positions (same)
shotDistances (int [1]) – Distance between shot indices.

Returns:

data – Data container with predefined sensor indices ‘s’ and ‘g’ for shot and receiver numbers.

Return type:

DataContainer

Examples using pygimli.physics.traveltime.createRAData

2D Refraction modelling and inversion

Refraction in 3D

Petrophysical joint inversion

pygimli.physics.traveltime.drawFirstPicks(ax, data, tt=None, plotva=False, **kwargs)[source]#

Plot first arrivals as lines.

Parameters:

ax (matplotlib.axes) – axis to draw the lines in
data (GIMLI::DataContainer) – data containing shots (“s”), geophones (“g”) and traveltimes (“t”). (:py:class:pygimli.physics.traveltime.DataContainerTT.)

Returns:

gci – list of plotting items (matplotlib lines)

Return type:

list

Examples using pygimli.physics.traveltime.drawFirstPicks

Field data inversion (“Koenigsee”)

Field data inversion ("Koenigsee")

pygimli.physics.traveltime.drawTravelTimeData(ax, data, t=None)[source]#

Draw first arrival traveltime data into mpl ax a.

data of type pg.DataContainer must contain sensorIdx ‘s’ and ‘g’ and thus being numbered internally [0..n)

pygimli.physics.traveltime.drawVA(ax, data, vals=None, usePos=True, pseudosection=False, **kwargs)[source]#

Draw apparent velocities as matrix into an axis.

Parameters:

ax (mpl.Axes)
data (pg.DataContainer()) – Datacontainer with ‘s’ and ‘g’ Sensorindieces and ‘t’ traveltimes.
usePos (bool [True]) – Use sensor positions for axes tick labels
pseudosection (bool [False]) – Show in pseudosection style.
vals (iterable) – Traveltimes, if None data need to contain ‘t’ values.

pygimli.physics.traveltime.load(fileName, verbose=False, **kwargs)[source]#

Shortcut to load TravelTime data.

Import Data and try to assume the file format.

TODO

add RHL class importer

Parameters:: fileName (str)
Returns:: data
Return type:: pg.DataContainer

pygimli.physics.traveltime.shotReceiverDistances(data, full=True)[source]#

Distance vector between shot and for each ‘s’ and ‘g’ in data.

Parameters:

data (pg.DataContainerERT)
full (bool [True]) – Get distances between shot and receiver position when full is True or only form x coordinate if full is False

Returns:

dists – Array of distances

Return type:

array

pygimli.physics.traveltime.show(data, **kwargs)[source]#: Show data.

Examples using pygimli.physics.traveltime.show

2D Refraction modelling and inversion

pygimli.physics.traveltime.showVA(data, usePos=True, ax=None, **kwargs)[source]#

Show apparent velocity as image plot.

Parameters:: data (pg.DataContainer()) – Datacontainer with ‘s’ and ‘g’ Sensorindieces and ‘t’ traveltimes.

Examples using pygimli.physics.traveltime.showVA

Crosshole traveltime tomography

Petrophysical joint inversion

pygimli.physics.traveltime.simulate(mesh, scheme, slowness=None, **kwargs)[source]#

Simulate traveltime measurements.

Perform the forward task for a given mesh, a slowness distribution (per cell) and return data (traveltime) for a measurement scheme.

Parameters:

mesh (GIMLI::Mesh) – Mesh to calculate for or use the last known mesh.
scheme (GIMLI::DataContainer) – Data measurement scheme needs ‘s’ for shot and ‘g’ for geophone data token.
slowness (array(mesh.cellCount()) | array(N, mesh.cellCount())) –
Slowness distribution for the given mesh cells can be:
- a single array of len mesh.cellCount()
- a matrix of N slowness distributions of len mesh.cellCount()
- a slowness map [[marker0, slow0], [marker1, slow1], …]
vel (array(mesh.cellCount()) | array(N, mesh.cellCount())) – Velocity distribution for the mesh cells (overwrites slowness!).
secNodes (int [2]) – Number of refinement nodes to increase accuracy of the forward calculation.
noiseLevel (float [0.0]) – Add relative noise to the simulated data. noiseLevel*100 in %
noiseAbs (float [0.0]) – Add absolute noise to the simulated data in ms.
seed (int [None]) – Seed the random generator for the noise.

Keyword Arguments:

returnArray ([False]) – Return only the calculated times.
verbose ([self.verbose]) – Overwrite verbose level.
**kwargs – Additional kwargs …

Returns:

t – The resulting simulated travel time values (returnArray=True) or DataContainer containing them in t field (returnArray=False). Either one column array or matrix in case of slowness matrix.

Return type:

array(N, data.size()) | DataContainer

Examples using pygimli.physics.traveltime.simulate

2D Refraction modelling and inversion

Crosshole traveltime tomography

Petrophysical joint inversion

Classes#

pygimli.physics.traveltime.DataContainer#: alias of DataContainerTT

class pygimli.physics.traveltime.DataContainerTT(data=None, **kwargs)[source]#

Bases: DataContainer

Data Container for traveltime.

__init__(data=None, **kwargs)[source]#: Initialize empty data container, load or copy existing.

class pygimli.physics.traveltime.Dijkstra#

Bases: instance

Dijkstras shortest path finding

class DistancePair_#

Bases: instance

Definition for the priority queue

__init__((object)arg1) → object :#

C++ signature :
void* __init__(_object*)

__init__( (object)arg1, (object)f, (object)s) -> object :

C++ signature :
void* __init__(_object*,double,GIMLI::Dijkstra::Edge_ {lvalue})

property first#

property second#

class Edge_#

Bases: instance

__init__((object)arg1) → object :#

C++ signature :
void* __init__(_object*)

__init__( (object)arg1, (object)a, (object)b) -> object :

C++ signature :
void* __init__(_object*,unsigned long,unsigned long)

property end#

property start#

__init__((object)arg1) → object :#

C++ signature :
void* __init__(_object*)

__init__( (object)arg1, (object)graph) -> object :

C++ signature :
void* __init__(_object*,std::__1::map<unsigned long, std::__1::map<unsigned long, GIMLI::GraphDistInfo, std::__1::less<unsigned long>, std::__1::allocator<std::__1::pair<unsigned long const, GIMLI::GraphDistInfo>>>, std::__1::less<unsigned long>, std::__1::allocator<std::__1::pair<unsigned long const, std::__1::map<unsigned long, GIMLI::GraphDistInfo, std::__1::less<unsigned long>, std::__1::allocator<std::__1::pair<unsigned long const, GIMLI::GraphDistInfo>>>>>>)

distance((object)arg1, (object)root, (object)node) → object :#

Distance from root to node.

C++ signature :
double distance(GIMLI::Dijkstra {lvalue},unsigned long,unsigned long)

distance( (object)arg1, (object)node) -> object :

Distance to node to the last known root.

C++ signature :: double distance(GIMLI::Dijkstra {lvalue},unsigned long)

distances((object)arg1, (object)root) → object :#

All distances to root.

C++ signature :
GIMLI::Vector<double> distances(GIMLI::Dijkstra {lvalue},unsigned long)

distances( (object)arg1) -> object :

All distances from to last known root.

C++ signature :: GIMLI::Vector<double> distances(GIMLI::Dijkstra {lvalue})

graph((object)arg1) → object :#

C++ signature :
std::__1::map<unsigned long, std::__1::map<unsigned long, GIMLI::GraphDistInfo, std::__1::less<unsigned long>, std::__1::allocator<std::__1::pair<unsigned long const, GIMLI::GraphDistInfo>>>, std::__1::less<unsigned long>, std::__1::allocator<std::__1::pair<unsigned long const, std::__1::map<unsigned long, GIMLI::GraphDistInfo, std::__1::less<unsigned long>, std::__1::allocator<std::__1::pair<unsigned long const, GIMLI::GraphDistInfo>>>>>> {lvalue} graph(GIMLI::Dijkstra {lvalue})

graph( (object)arg1) -> object :

C++ signature :
std::__1::map<unsigned long, std::__1::map<unsigned long, GIMLI::GraphDistInfo, std::__1::less<unsigned long>, std::__1::allocator<std::__1::pair<unsigned long const, GIMLI::GraphDistInfo>>>, std::__1::less<unsigned long>, std::__1::allocator<std::__1::pair<unsigned long const, std::__1::map<unsigned long, GIMLI::GraphDistInfo, std::__1::less<unsigned long>, std::__1::allocator<std::__1::pair<unsigned long const, GIMLI::GraphDistInfo>>>>>> graph(GIMLI::Dijkstra {lvalue})

graphInfo((object)arg1, (object)na, (object)nb) → object :#

C++ signature :: GIMLI::GraphDistInfo graphInfo(GIMLI::Dijkstra {lvalue},unsigned long,unsigned long)

setGraph((object)arg1, (object)graph) → object :#

C++ signature :: void* setGraph(GIMLI::Dijkstra {lvalue},std::__1::map<unsigned long, std::__1::map<unsigned long, GIMLI::GraphDistInfo, std::__1::less<unsigned long>, std::__1::allocator<std::__1::pair<unsigned long const, GIMLI::GraphDistInfo>>>, std::__1::less<unsigned long>, std::__1::allocator<std::__1::pair<unsigned long const, std::__1::map<unsigned long, GIMLI::GraphDistInfo, std::__1::less<unsigned long>, std::__1::allocator<std::__1::pair<unsigned long const, GIMLI::GraphDistInfo>>>>>>)

setStartNode((object)arg1, (object)startNode) → object :#

C++ signature :: void* setStartNode(GIMLI::Dijkstra {lvalue},unsigned long)

shortestPath((object)arg1, (object)start, (object)end) → object :#

Get the shortest way from node index start to end.

C++ signature :: GIMLI::Vector<unsigned long> shortestPath(GIMLI::Dijkstra {lvalue},unsigned long,unsigned long)

shortestPathTo((object)arg1, (object)node, (object)way) → object :#

Get the shortest way from root to node. Inline version.

C++ signature :
void* shortestPathTo(GIMLI::Dijkstra {lvalue},unsigned long,GIMLI::Vector<unsigned long> {lvalue})

shortestPathTo( (object)arg1, (object)node) -> object :

Get the shortest way from root to node.

C++ signature :: GIMLI::Vector<unsigned long> shortestPathTo(GIMLI::Dijkstra {lvalue},unsigned long)

pygimli.physics.traveltime.Manager#: alias of TravelTimeManager

class pygimli.physics.traveltime.RefractionNLayer(offset=0, nlay=3, vbase=1100, verbose=True)[source]#

Bases: ModellingBaseMT__

Forward operator for 1D Refraction seismic with layered model.

__init__(offset=0, nlay=3, vbase=1100, verbose=True)[source]#

Init forward operator. Model are velocity increases.

Parameters:

offset (iterable) – vector of offsets between shot and geophone
nlay (int) – number of layers
vbase (float) – base velocity (all values are above)

response(model)[source]#: Return forward response f(m).

thkVel(model)[source]#: Return thickness and velocity vectors from model.

class pygimli.physics.traveltime.RefractionNLayerFix1stLayer(offset=0, nlay=3, v0=1465, d0=200, muteDirect=False, verbose=True)[source]#

Bases: ModellingBaseMT__

FOP for 1D Refraction seismic with layered model (e.g. water layer).

__init__(offset=0, nlay=3, v0=1465, d0=200, muteDirect=False, verbose=True)[source]#

Init forward operator for velocity increases with fixed 1st layer.

Parameters:

offset (iterable) – vector of offsets between shot and geophone
nlay (int) – number of layers
v0 (float) – First layer velocity (at the same time base velocity)
d0 (float) – Depth of first layer in meter.
muteDirect (bool [False]) – Mute the direct arrivels fron the first layer.

response(model)[source]#: Return forward response f(m).

thkVel(model)[source]#: Return thickness and velocity vectors from model.

class pygimli.physics.traveltime.TravelTimeDijkstraModelling(**kwargs)[source]#

Bases: MeshModelling

Forward modelling class for traveltime using Dijktras method.

__init__(**kwargs)[source]#

Initialize.

Variables:

fop (pg.frameworks.Modelling)
data (pg.DataContainer)
modelTrans ([pg.trans.TransLog()])

Parameters:

**kwargs – fop : Modelling

createGraph(slowness)[source]#: Create Dijkstra graph.

createJacobian(par)[source]#: Create Jacobian (way matrix).

createRefinedFwdMesh(mesh)[source]#

Refine the current mesh for higher accuracy.

This is called automatic when accesing self.mesh() so it ensures any effect of changing region properties (background, single).

createStartModel(dataVals)[source]#: Create a starting model from data values (gradient or constant).

property dijkstra#: Return current Dijkstra graph associated to mesh and model.

drawData(ax, data=None, **kwargs)[source]#

Draw the data (as apparent velocity crossplot by default).

Parameters:: data (pg.DataContainer)

drawModel(ax, model, **kwargs)[source]#: Draw the model.

response(par)[source]#: Return forward response (simulated traveltimes).

setDataPost(data)[source]#: Set data after forward operator has been initalized.

setMeshPost(mesh)[source]#: Set mesh after forward operator has been initalized.

way(s, g)[source]#

Return node indices for the way from the shot to the receiver.

The index is based on the given data, mesh and last known model.

class pygimli.physics.traveltime.TravelTimeManager(data=None, **kwargs)[source]#

Bases: MeshMethodManager

Manager for refraction seismics (traveltime tomography).

TODO Document main members and use default MethodManager interface e.g., self.inv, self.fop, self.paraDomain, self.mesh, self.data

__init__(data=None, **kwargs)[source]#

Create an instance of the Traveltime manager.

Parameters:: data (GIMLI::DataContainer | str) – You can initialize the Manager with data or give them a dataset when calling the inversion.

applyMesh(mesh, secNodes=None, ignoreRegionManager=False)[source]#: Apply mesh, i.e. set mesh in the forward operator class.

checkData(data)[source]#: Return data from container.

checkError(err, dataVals)[source]#: Return relative error.

createForwardOperator(**kwargs)[source]#

Create default forward operator for Traveltime modelling.

Your want your Manager use a special forward operator you can add them here on default Dijkstra is used.

createMeshMovedToMeshManager(data=None, **kwargs)[source]#

Create default inversion mesh.

Inversion mesh for traveltime inversion does not need boundary region.

Parameters:: data (DataContainer) – Data container to read sensors from.
Keyword Arguments:: ` (Forwarded to)

createTraveltimefield(v=None, startPos=None, withSec=False)[source]#: Compute a single traveltime field.

drawRayPaths(ax, model=None, rayPaths=None, **kwargs)[source]#

Draw the the ray paths for model or last model.

If model is not specified, the last calculated Jacobian is used.

Parameters:

rayPaths (list of np.array) – x/y column array with ray point positions
model (array) – Velocity model for which to calculate and visualize ray paths (the default is model for last Jacobian calculation in self.velocity).
ax (matplotlib.axes object) – To draw the model and the path into.
**kwargs (type) – Additional arguments passed to LineCollection (alpha, linewidths, color, linestyles).

Returns:

lc

Return type:

matplotlib.LineCollection

getRayPaths(model=None)[source]#

Compute ray paths.

If model is not specified, the last calculated Jacobian is used.

Parameters:: model (array) – Velocity model for which to calculate and visualize ray paths (the default is model for last Jacobian calculation in self.velocity).
Return type:: list of two-column array holding x and y positions

invert(data=None, useGradient=True, vTop=500, vBottom=5000, secNodes=None, **kwargs)[source]#

Invert data.

Parameters:

data (pg.DataContainer()) – Data container with at least SensorIndices ‘s g’ (shot/geophone) & data values ‘t’ (traveltime in s) and ‘err’ (absolute error in s)
useGradient (bool [True]) – Use gradient starting model typical for refraction cases. For crosshole tomography geometry you should set this to False for a non-gradient (e.g. homogeneous) starting model.
vTop (float) – Top velocity for gradient starting model.
vBottom (float) – Bottom velocity for gradient starting model.
secNodes (int [2]) – Number of secondary nodes for accuracy of forward computation.

Returns:

Mapped (for paradomain) velocity model.

Return type:

model

Keyword Arguments:

kwargs (**) – Inversion related arguments: See pygimli.frameworks.MeshMethodManager.invert

load(fileName)[source]#: Load any supported data file.

rayCoverage()[source]#: Ray coverage, i.e. summed raypath lengths.

saveResult(folder=None, size=(16, 10), verbose=False, **kwargs)[source]#

Save the results in a specified (or date-time derived) folder.

Saved items are:

Resulting inversion model
Velocity vector
Coverage vector
Standardized coverage vector
Mesh (bms and vtk with results)

Parameters:

path (str[None]) – Path to save into. If not set the name is automatically created
size ((float, float) (16,10)) – Figure size.

Keyword Arguments:

showResults (Will be forwarded to)

Returns:

Name of the result path.

Return type:

str

showCoverage(ax=None, name='coverage', **kwargs)[source]#: Show the ray coverage in log-scale.

showFit(axs=None, firstPicks=True, **kwargs)[source]#: Show data fit as first-break picks or apparent velocity.

showRayPaths(model=None, ax=None, **kwargs)[source]#

Show the model with ray paths for given model.

If not model specified, the last calculated Jacobian is taken.

Parameters:

model (array) – Velocity model for which to calculate and visualize ray paths (the default is model for last Jacobian calculation in self.velocity).
ax (matplotlib.axes object) – To draw the model and the path into.
**kwargs (type) – forward to drawRayPaths

Returns:

ax (matplotlib.axes object)
cb (matplotlib.colorbar object (only if model is provided))

Examples

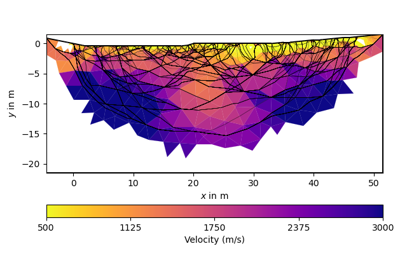
>>> import pygimli as pg
>>> from pygimli.physics import traveltime as tt
>>>
>>> x, y = 8, 6
>>> mesh = pg.createGrid(x, y)
>>> data = tt.createRAData([(0, 0)] + [(x, i) for i in range(y)],
...                       shotDistance=y+1)
>>> data["t"] = 1.0
>>> mgr = tt.Manager(data)
>>> mgr.applyMesh(mesh, secNodes=10)
>>> ax, cb = mgr.showRayPaths(showMesh=True, diam=0.1)

(png, pdf)

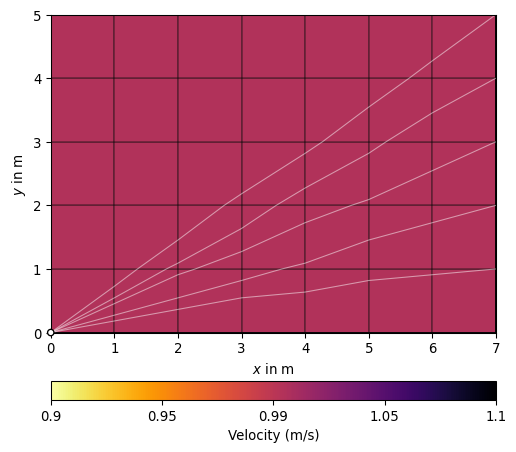
../../_images/pygimli-physics-traveltime-1.png

simulate(mesh=None, scheme=None, slowness=None, vel=None, seed=None, secNodes=2, noiseLevel=0.0, noiseAbs=0.0, **kwargs)[source]#

Simulate traveltime measurements.

Perform the forward task for a given mesh, a slowness distribution (per cell) and return data (traveltime) for a measurement scheme.

Parameters:

mesh (GIMLI::Mesh) – Mesh to calculate for or use the last known mesh.
scheme (GIMLI::DataContainer) – Data measurement scheme needs ‘s’ for shot and ‘g’ for geophone data token.
slowness (array(mesh.cellCount()) | array(N, mesh.cellCount())) –
Slowness distribution for the given mesh cells can be:
- a single array of len mesh.cellCount()
- a matrix of N slowness distributions of len mesh.cellCount()
- a slowness map [[marker0, slow0], [marker1, slow1], …]
vel (array(mesh.cellCount()) | array(N, mesh.cellCount())) – Velocity distribution for the mesh cells (overwrites slowness!).
secNodes (int [2]) – Number of refinement nodes to increase accuracy of the forward calculation.
noiseLevel (float [0.0]) – Add relative noise to the simulated data. noiseLevel*100 in %
noiseAbs (float [0.0]) – Add absolute noise to the simulated data in ms.
seed (int [None]) – Seed the random generator for the noise.

Keyword Arguments:

returnArray ([False]) – Return only the calculated times.
verbose ([self.verbose]) – Overwrite verbose level.
**kwargs – Additional kwargs …

Returns:

t – The resulting simulated travel time values (returnArray=True) or DataContainer containing them in t field (returnArray=False). Either one column array or matrix in case of slowness matrix.

Return type:

array(N, data.size()) | DataContainer

standardizedCoverage()[source]#: Standardized coverage vector (0|1) using neighbor info.

property velocity#: Return velocity vector (the inversion model).

pygimli.physics.traveltime.TravelTimeModelling#: alias of TravelTimeDijkstraModelling