Note
Go to the end to download the full example code.
3D Darcy flow#
Here we illustrate Darcy flow in a heterogeneous 3D body. We use the general
pygimli.solver.solveFiniteElements() to solve Darcy’s law:
The sought hydraulic velocity distribution can then be calculated as the gradient field of \(\mathbf{v}=-\nabla p\).
import numpy as np
import pygimli as pg
import pygimli.meshtools as mt
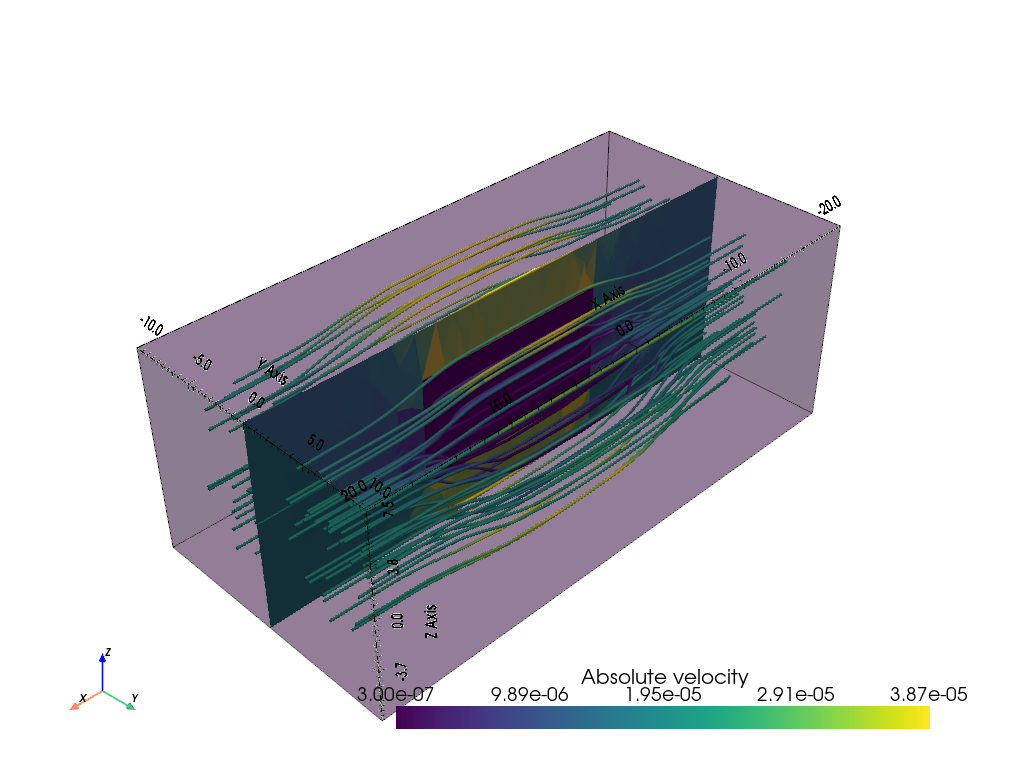
from pygimli.viewer.pv import drawStreamLines, drawSlice
We start with creating the geometry: a small cube inside of a bigger one, and create a mesh from it.
plc = mt.createCube(size=[40, 20, 15], marker=1, boundaryMarker=0)
cube = mt.createCube(size=[15, 15, 8], marker=2, boundaryMarker=0)
geom = plc + cube
mesh = mt.createMesh(geom, area=4)
For the boundary conditions, we set the markers of all left boundaries to 1 and the markers of all righth boundaries to 2.
Next, we create a map for the hydraulic conductivity. The outer cube has 1e-4m/s and the inner 1e-6m/s.
We set two different heads for the left and right bounday and solve the Darcy equation using Finite Elements
From the hydraulic head we compute the velocity by multiplying it with the hydraulic conductivity that is before transformed into an isotropic tensor.
kTensor = np.column_stack([kArray] * 3)
vel = -pg.solver.grad(mesh, h) * kTensor
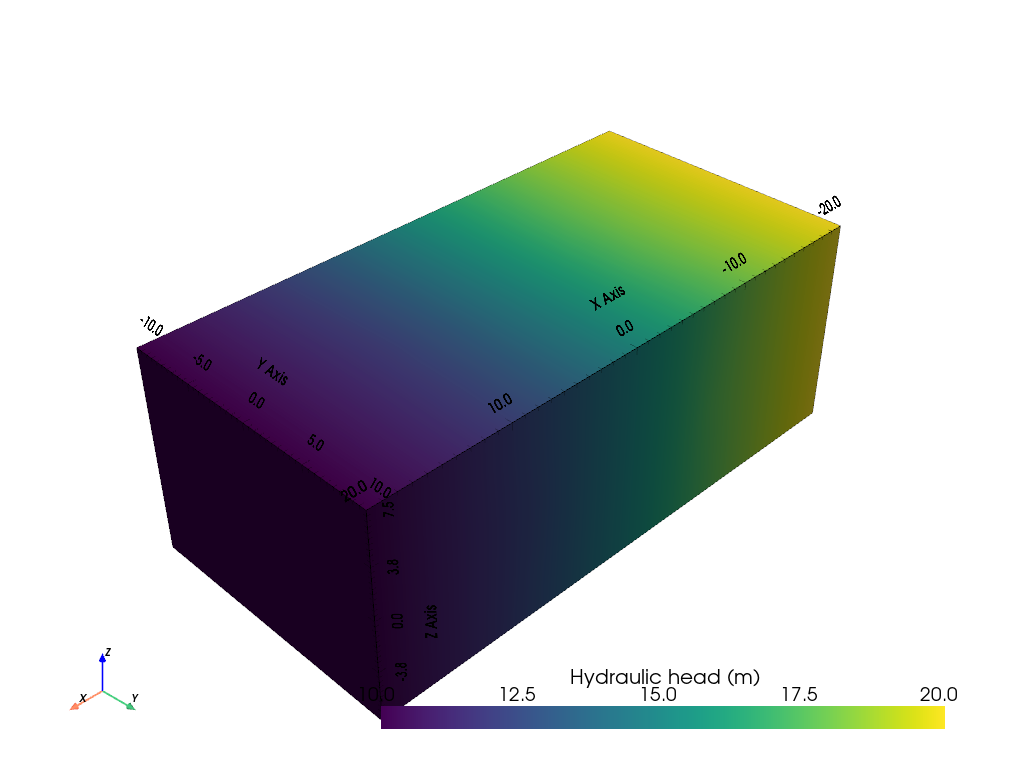
pg.show(mesh, h, label="Hydraulic head (m)")
(<pyvista.plotting.plotter.Plotter object at 0x323670b60>, None)
Last, we show the flow lines that avoid the poor conductor.